题目内容
 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则△AEF的周长为
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则△AEF的周长为考点:三角形中位线定理,矩形的性质
专题:
分析:先求出矩形的对角线AC,根据中位线定理可得出EF,继而可得出△AEF的周长.
解答:解:在Rt△ABC中,AC=
=13cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
EF=
OD=
BD=
AC=
cm,
AF=
AD=
BC=6cm,
AE=
AO=
AC=
cm,
∴△AEF的周长=AE+AF+EF=
+6+
=
(cm).
故答案是:
.
| AB2+BC2 |
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
EF=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 13 |
| 4 |
AF=
| 1 |
| 2 |
| 1 |
| 2 |
AE=
| 1 |
| 2 |
| 1 |
| 4 |
| 13 |
| 4 |
∴△AEF的周长=AE+AF+EF=
| 13 |
| 4 |
| 13 |
| 4 |
| 25 |
| 2 |
故答案是:
| 25 |
| 2 |
点评:本题考查了三角形的中位线定理、勾股定理及矩形的性质,解答本题需要我们熟练掌握三角形中位线的判定与性质.

练习册系列答案
相关题目
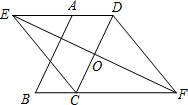 如图,平行四边形ABCD的边CD的垂直平分线与边DA,BC的延长线分别交于点E,F,与边CD交于点O,连结CE,DF.
如图,平行四边形ABCD的边CD的垂直平分线与边DA,BC的延长线分别交于点E,F,与边CD交于点O,连结CE,DF. 如图,AB⊥CD,CD⊥BD,∠A=∠FEC.以下是小贝同学证明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由.
如图,AB⊥CD,CD⊥BD,∠A=∠FEC.以下是小贝同学证明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由. 如图,正方形ABCD中,E是AD的中点,AB=8,M是线段CE上的动点,则BM的最小值是
如图,正方形ABCD中,E是AD的中点,AB=8,M是线段CE上的动点,则BM的最小值是 如图,△ABC的边BC,AC的垂直平分线相交于点O,连接AO,BO.若∠C=40°,则∠AOB的度数为
如图,△ABC的边BC,AC的垂直平分线相交于点O,连接AO,BO.若∠C=40°,则∠AOB的度数为