Question

10．（1）如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．探究线段PD、PF的关系，并加以证明．
（2）如图2，将正方形CGEF绕点C旋转任意角度后，其他条件不变，探究：线段PD，PF的关系，并加以证明．

Answer 1

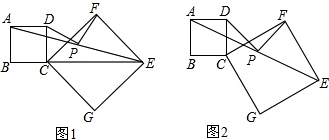
分析 （1）根据已知条件证明△DCF≌△NEF，证明出线段DF与线段FN相等，从而证出△FDN为等腰三角形，再根据条件证明△ADM≌△ENM，所以DM=MN．进而求出线段MD、MF的关系；
（2）延长DP到N，使PN=PD，连接FD、FN、EN，延长EN与DC延长线交于点H．证明△DCF≌△NEF，即可得到线段PD，PF的位置及数量关系．

解答 证明：（1）延长DP交BE于N，连接FD、FN，
∵CE是正方形CGEF的对角线，
∴CF=EF，∠1=∠FEN=45°，
又∵∠BCD=90°，
∴∠DCE=90°，
∴∠2=∠1=∠FEN=45°，
在△CDF和△ENF中，
$\left\{\begin{array}{l}{CD=EN}\\{∠2=∠NEF}\\{CF=EF}\end{array}\right.$，
∴△CDF≌△ENF（SAS）
∴∠3=∠4，DF=FN，
又∵∠CFN+∠4=90°，
∴∠CFN+∠3=90°，
∴△DFN是等腰直角三角形，
在△ADP与△ENP中，
$\left\{\begin{array}{l}{∠DAP=∠PEN}\\{AP=PE}\\{∠DPA=∠EPN}\end{array}\right.$
∵△ADP≌△ENP，
∴DP=NP，
∴FP=D，FP⊥DP；

（2）PD=PF，PD⊥PF，
延长DP到N，使PN=PD，连接FD、FN、EN，延长EN与DC延长线交于点H．
在△APD与△EPN中，
$\left\{\begin{array}{l}{PA=PE}\\{∠1=∠2}\\{PD=PN}\end{array}\right.$，
∴△APD≌△EPN，
∴∠3=∠4，AD=NE．
又∵正方形ABCD、CGEF，
∴CF=EF，AD=DC，∠ADC=90°，
∠CFE=∠ADC=∠FEG=∠FCG=90°．
∴DC=NE．
∵∠3=∠4，
∴AD∥EH．
∴∠H=∠ADC=90°．
∵∠G=90°，∠5=∠6，
∴∠7=∠8．
∵∠7+∠DCF=∠8+∠FEN=90°，
∴∠DCF=∠FEN．
在△DCF与△NEF中，
$\left\{\begin{array}{l}{CD=NE}\\{∠DCF=∠FEN}\\{FC=FE}\end{array}\right.$，
∴△DCF≌△NEF，
∴FD=FN，∠DFC=∠NFE．
∵∠CFE=90°，
∴∠DFN=90°，
∴FP⊥PD，PF=PD．

点评 本题考查了正方形的性质，等腰三角形的性质，全等三角形的判定与性质，等腰三角形三线合一的性质，直角三角形斜边上的中线等于斜边的一半的性质，综合性较强，需要两次利用三角形全等证明，思路比较繁琐．