题目内容
1．若关于x的方程（x2-2x+k）（x2-3x+k+4）（x2-4x-k+8）=0有实根，求实根并求k的取值范围．分析 根据题意，（x2-2x+k）=0、（x2-3x+k+4）=0，（x2-4x-k+8）=0其中一个有实根即可，反之，都无解，由此利用根的判别式逐一判定得出k的取值范围，进一步得出答案即可．
解答 解：要使x的方程（x2-2x+k）（x2-3x+k+4）（x2-4x-k+8）=0无实根，
即（x2-2x+k）=0、（x2-3x+k+4）=0（x2-4x-k+8）=0无实根即可，
∵△1=4-k＜0，△2=9-4（k+4）＜0，△3=16-4（-k+8）＜0，
∴k＞1，k＞-$\frac{7}{4}$，k＜4，
∴1＜k＜4，
∴方程有解的k的取值范围为k≤1，k≥4．
点评 此题考查根的判别式的灵活运用，从反面考虑是解决问题的关键．
练习册系列答案
相关题目
如图，正方形网格中每个小正方形的边长都是1，每个小格的格点叫做“格点”，以格点为顶点分别按下列要求画出三角形．
如图，在△ABC中，以AB为直径的⊙O交AC于点D，过点D作DE⊥BC于点E，且∠BDE=∠A．
6．
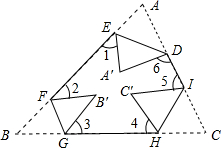如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（ ）
如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（ ）| A． | 180° | B． | 270° | C． | 360° | D． | 540° |
13．
某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．
（1）根据题意，填写如表：
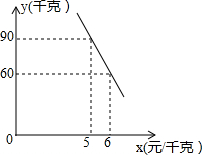
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．（1）根据题意，填写如表：
| 蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
| 所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
