题目内容
 如图正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°.
如图正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°.
(1)求证:BE+DF=EF;
(2)若BE=3,DF=2,求AB的长.
 (1)证明:延长EB至H,使BH=DF,连接AH,
(1)证明:延长EB至H,使BH=DF,连接AH,∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
∵

∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
∵

∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
(2)解:∵EF=BE+DF,BE=3,DF=2,∴EF=5,
设AB=x,则CE=x-3,CF=x-2,
在△CEF中:FC2+EC2=EF2,
故(x-2)2+( x-3)2=52,
解得:x1=-1(舍去),x2=6,
∴AB=6.
分析:(1)延长EB至H,使BH=DF,连接AH,证△ADF≌△ABH,△FAE≌△HAE,根据全等三角形的性质得出EF=HE=BE+HB进而求出即可;
(2)根据全等三角形的性质及勾股定理即可求得正方形的边长.
点评:本题主要考查正方形的性质,全等三角形的判定以及勾股定理的综合应用.作出辅助线延长EB至H,使BH=DF,利用全等三角形性质与判定求出是解题关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 12、如图正方形ABCD中,以D为圆心,DC为半径作弧与以BC为直径的⊙O交于点P,⊙O交AC于E,CP交AB于M,延长AP交⊙O于N,下列结论:①AE=EC;②PC=PN;③EP⊥PN;④ON∥AB,其中正确的是( )
12、如图正方形ABCD中,以D为圆心,DC为半径作弧与以BC为直径的⊙O交于点P,⊙O交AC于E,CP交AB于M,延长AP交⊙O于N,下列结论:①AE=EC;②PC=PN;③EP⊥PN;④ON∥AB,其中正确的是( )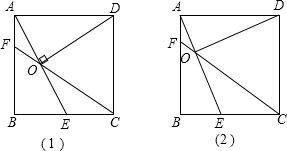 点F.
点F. 如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F.求证:点F是CD边的中点.
如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F.求证:点F是CD边的中点. 已知:如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF
已知:如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF 如图正方形ABCD中,E是BC边的中点,AE与BD相交于F点,△DEF的面积是1,那么正方形ABCD的面积是
如图正方形ABCD中,E是BC边的中点,AE与BD相交于F点,△DEF的面积是1,那么正方形ABCD的面积是