题目内容
如图正方形ABCD中，E是BC边的中点，AE与BD相交于F点，△DEF的面积是1，那么正方形ABCD的面积是6
6
．分析：先设△BEF的面积是x，由于E是BC中点，那么S△DBE=S△DCE，易求S正方形=4（1+x），又四边形ABCD是正方形，那么
AD∥BC，AD=BC，根据平行线分线段成比例定理的推论可得△BEF∽△DAF，于是S△BEF：S△DAF=（
）2，E是BC中点可知BE：AD=1：2，于是S△DAF=4x，进而可得S正方形=S△ABF+S△BEF+S△ADF+S△DEF+S△DCE=1+x+4x+1+1+x，等量代换可得4（1+x）=1+x+4x+1+1+x，解可求x，进而可求正方形的面积．
AD∥BC，AD=BC，根据平行线分线段成比例定理的推论可得△BEF∽△DAF，于是S△BEF：S△DAF=（
| BE |
| AD |
解答：解：如右图，设△BEF的面积是x，
∵E是BC中点，
∴S△DBE=S△DCE，
∴S△BCD=2（1+x），
∴S正方形=4（1+x），
∵四边形ABCD是正方形，
∴AD∥BC，AD=BC，
∴△BEF∽△DAF，
∴S△BEF：S△DAF=（
）2，
∵E是BC中点，
∴BE=CE，
∴BE：AD=1：2，
∴S△DAF=4x，
∵S△ABE=S△BED，
∴S△ABF=S△DEF=1，
∴S正方形=S△ABF+S△BEF+S△ADF+S△DEF+S△DCE=1+x+4x+1+1+x，
∴4（1+x）=1+x+4x+1+1+x，
解得x=0.5，
∴S正方形=4（1+x）=4（1+0.5）=6．
∵E是BC中点，
∴S△DBE=S△DCE，
∴S△BCD=2（1+x），
∴S正方形=4（1+x），
∵四边形ABCD是正方形，
∴AD∥BC，AD=BC，
∴△BEF∽△DAF，
∴S△BEF：S△DAF=（
| BE |
| AD |
∵E是BC中点，
∴BE=CE，
∴BE：AD=1：2，
∴S△DAF=4x，
∵S△ABE=S△BED，
∴S△ABF=S△DEF=1，
∴S正方形=S△ABF+S△BEF+S△ADF+S△DEF+S△DCE=1+x+4x+1+1+x，
∴4（1+x）=1+x+4x+1+1+x，
解得x=0.5，
∴S正方形=4（1+x）=4（1+0.5）=6．
点评：本题考查了面积以及等积变换、相似三角形的判定和性质，解题的关键是找出正方形面积的两种表示方式．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
12、如图正方形ABCD中，以D为圆心，DC为半径作弧与以BC为直径的⊙O交于点P，⊙O交AC于E，CP交AB于M，延长AP交⊙O于N，下列结论：①AE=EC；②PC=PN；③EP⊥PN；④ON∥AB，其中正确的是（ ）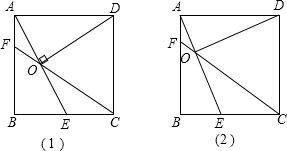
点F．
如图正方形ABCD中，E为AD边上的中点，过A作AF⊥BE，交CD边于F．求证：点F是CD边的中点．
已知：如图正方形ABCD中，E为CD边上一点，F为BC延长线上一点，且CE=CF