题目内容
1.已知9m=$\frac{2}{3}$,3n=$\frac{1}{2}$;则下列结论正确的是( )| A. | 2m-n=$\frac{4}{3}$ | B. | 2m+n=-1 | C. | 2m-n=3 | D. | $\frac{2m}{n}$=3 |
分析 首先根据幂的乘方的法则把出9m变形为32m,然后按照同底数幂的乘法法则求解.
解答 解:因为9m=32m=$\frac{2}{3}$,3n=$\frac{1}{2}$;
所以可得:32m•3n=32m+n=$\frac{1}{3}$,
所以可得:2m+n=-1;
故选B
点评 本题考查了幂的乘方和同底数幂的乘法,解答本题的关键是掌握幂的乘方和同底数幂的乘法法则.

练习册系列答案
相关题目
13.分式-$\frac{1}{1-x}$可变形为( )
| A. | -$\frac{1}{x-1}$ | B. | $\frac{1}{1+x}$ | C. | -$\frac{1}{1+x}$ | D. | $\frac{1}{x-1}$ |
9.已知x2-5xy+6y2=0,则x:y等于( )
| A. | $\frac{1}{3}$或$\frac{1}{2}$ | B. | 2或3 | C. | $\frac{1}{6}$或1 | D. | 6或1 |
6.根据下面表格中的取值,方程x2+x-3=0有一个根的近似值(精确到0.1)是( )
| x | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+x-3 | -0.36 | -0.01 | 0.36 | 0.75 |
| A. | 1.5 | B. | 1.2 | C. | 1.3 | D. | 1.4 |
13.七边形的对角线共有( )
| A. | 10条 | B. | 15条 | C. | 21条 | D. | 14条 |
11.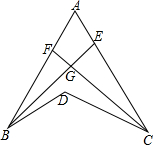 如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
 如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
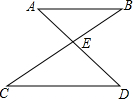 如图,AB∥CD,AD与BC交于点E.若∠B=35°,∠D=45°,则∠AEC=80°.
如图,AB∥CD,AD与BC交于点E.若∠B=35°,∠D=45°,则∠AEC=80°.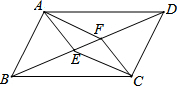 已知:如图,在?ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F.证明:四边形AECF是平行四边形.
已知:如图,在?ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F.证明:四边形AECF是平行四边形.