题目内容
 如图,在△ABC中,MN是AB的中垂线,BN=
如图,在△ABC中,MN是AB的中垂线,BN=| 6 |
考点:解直角三角形,线段垂直平分线的性质
专题:
分析:根据线段垂直平分线的性质首先求出AN的长度,进而求出∠CAN的度数;结合∠C=60°,作出CN边上的高,根据三角形的边角关系及勾股定理求出线段AD、CN的长度即可解决问题.
解答:解:如图,过点A作AD⊥CN于点D;
∵MN是AB的中垂线,∴NA=NB,∠NAB=∠NBA=22.5°;
故∠DNA=∠NAB+∠NBA=45°,
∴∠DAN=90°-45°=45°,∠DNA=∠DAN,
故DA=DN(设为x),由勾股定理得:x2+x2=(
)2,
解得x=
;在直角△ADC中,tanC=
,故CD=
=
=1;
∴△ANC的面积=
(
+1)×
=

∵MN是AB的中垂线,∴NA=NB,∠NAB=∠NBA=22.5°;
故∠DNA=∠NAB+∠NBA=45°,
∴∠DAN=90°-45°=45°,∠DNA=∠DAN,
故DA=DN(设为x),由勾股定理得:x2+x2=(
| 6 |
解得x=
| 3 |
| AD |
| CD |
| AD |
| tan60° |
| ||
|
∴△ANC的面积=
| 1 |
| 2 |
| 3 |
| 3 |
3+
| ||
| 2 |

点评:命题考查了线段垂直平分线的性质、三角形的边角关系、勾股定理及其应用等问题;解题的关键是:根据题意求出∠CNA=45°,作出三角形的高线;对综合思维能力提出了较高要求.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
若正方形的对角线长为2cm,则这个正方形的面积为( )
| A、4cm2 | ||
| B、2cm2 | ||
C、
| ||
D、2
|
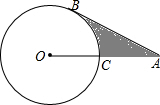 如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
 如图,△ABC的面积为
如图,△ABC的面积为 如图,AD平分∠CAE,∠B=35°,∠DAE=60°,求∠ACD的度数.
如图,AD平分∠CAE,∠B=35°,∠DAE=60°,求∠ACD的度数.