题目内容
一个边长为2的等边三角形,它的角平分线相交于原点,求三角形的三个顶点在直角坐标系中的坐标.
考点:等边三角形的性质,坐标与图形性质
专题:
分析:不妨设三角形的三个顶点分别为A、B、C,A在y轴的正半轴上,BC交y轴于点D,由勾股定理求得AD的长,由题可知原点O为三角形的重心,由可求AO和BO的长,则可写出三点的坐标.
解答:
解:如图△ABC,A在y轴的正半轴上,BC交y轴于点D,
AB=BC=AC=2,则BD=CD=1,
在Rt△ABD中由勾股定理可求得AD=
,
由题意可知O为△ABC的重心,所以AO=
AD=
,OD=
,
所以A点坐标为(0,
),B点坐标为(-1,-
),C点坐标为(1,-
).

解:如图△ABC,A在y轴的正半轴上,BC交y轴于点D,
AB=BC=AC=2,则BD=CD=1,
在Rt△ABD中由勾股定理可求得AD=
| 3 |
由题意可知O为△ABC的重心,所以AO=
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
所以A点坐标为(0,
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查等三边三角形的性质,由题意得出O为三角形的重心求出AO的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
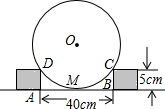 如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm.
如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm. 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1= 如图,在△ABC中,MN是AB的中垂线,BN=
如图,在△ABC中,MN是AB的中垂线,BN= 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=
如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=