题目内容
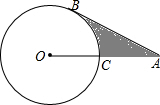 如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.(1)求
 |
| BC |
(2)设圆O的半径为5,求图中阴影部分面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OB、BC,根据切线的性质求得OB⊥AB,根据直角三角形斜边中线的性质得出BC=
OA,进而求得OB=BC=OC,得出△OBC是等边三角形,
求得∠BOC=60°,即可求得
的度数;
(2)先求得直角三角形的面积和扇形的面积,根据S阴影=S△AOB-S扇形即可求得.
| 1 |
| 2 |
求得∠BOC=60°,即可求得
 |
| BC |
(2)先求得直角三角形的面积和扇形的面积,根据S阴影=S△AOB-S扇形即可求得.
解答: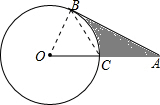 解:(1)连接OB、BC,
解:(1)连接OB、BC,
∵AB是圆O的切线,切点为B,
∴OB⊥AB,
∵AC=OC.
∴BC=
OA,
∵AC=OC=
OA,
∴OB=BC=OC,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴
的度数为60°;
(2)∵∠BOC=60°,OA=10,
∴AB=sin60°•OA=
×10=5
,
∴S△AOB=
AB•OB=
×5
×5=
,
∵S扇形=
×60=
,
∴S阴影=S△AOB-S扇形=
.
 解:(1)连接OB、BC,
解:(1)连接OB、BC,∵AB是圆O的切线,切点为B,
∴OB⊥AB,
∵AC=OC.
∴BC=
| 1 |
| 2 |
∵AC=OC=
| 1 |
| 2 |
∴OB=BC=OC,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴
 |
| BC |
(2)∵∠BOC=60°,OA=10,
∴AB=sin60°•OA=
| ||
| 2 |
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
25
| ||
| 2 |
∵S扇形=
| π•OB2 |
| 360 |
| 25π |
| 6 |
∴S阴影=S△AOB-S扇形=
75
| ||
| 6 |
点评:本题考查了切线的性质,扇形面积的计算,解题的根据是连接OB,构建直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一家商店一月份把某种进货价为100元的商品,提高60%出售,到三月份再声称以8折(80%)大拍卖,那么该商品三月份的价格比进货价( )
| A、高12.8%元 |
| B、低12.8%元 |
| C、高40元 |
| D、高28元 |
可以由抛物线y=x2平移得到抛物线y=(x-2)2+1,下列平移方法中正确的是( )
| A、向右平移2个单位,再向上平移1个单位 |
| B、向右平移2个单位,再向下平移1个单位 |
| C、向左平移2个单位,再向上平移1个单位 |
| D、向左平移2个单位,再向下平移1个单位 |
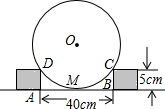 如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm.
如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm. 如图,在△ABC中,MN是AB的中垂线,BN=
如图,在△ABC中,MN是AB的中垂线,BN=