题目内容
等腰三角形顶角的度数是底角的4倍，底边长为a，则其腰上的高为 ．
考点：解直角三角形
专题：计算题
分析：设底角的度数为x，则顶角的度数为4x，根据三角形内角和定理可计算出x=30°，即得到∠BCA=30°，然后根据含30度的直角三角形三边的关系求解．
解答：解：
如图，
设底角的度数为x，则顶角的度数为4x，
根据题意得4x+x+x=180°，解得x=30°，
所以∠BCA=30°，
t△BCD中，BC=a，
所以BD=
a．
故答案为
a．
如图，设底角的度数为x，则顶角的度数为4x，
根据题意得4x+x+x=180°，解得x=30°，
所以∠BCA=30°，
t△BCD中，BC=a，
所以BD=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，若AB=2，AD=3，则tanB的值为在以∠C为直角的三角形中，有两边分别为3和6，则sinA不可能是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列等式中：
（1）（a+b）2=a2+b2；
（2）（x-a）（x+b）=x2-（a+b）x-ab；
（3）2a2•2a-1=a；
（4）2a3÷（2a3-a2）=1-2a．
其中不成立的有（ ）
（1）（a+b）2=a2+b2；
（2）（x-a）（x+b）=x2-（a+b）x-ab；
（3）2a2•2a-1=a；
（4）2a3÷（2a3-a2）=1-2a．
其中不成立的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
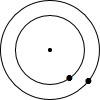如图，有2个同心圆，半径分别为R和r（单位：厘米），且R＞r＞1，记两圆之间的圆环面积为P；若把R和r都增加1厘米，记两圆之间的圆环面积为Q，则（ ）A、0＜
| ||
B、1＜
| ||
C、2＜
| ||
D、3＜
|
