题目内容
6.如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm,线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动,过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0)(1)用含t的代数式表示线段EF的长度;
(2)在运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,试说明理由.
分析 (1)由BD=tcm,DE=4cm,可得BE=BD+DE=(t+4)cm,又由EF∥AC,即可得△BEF∽△BAC,然后根据相似三角形的对应边成比例,即可求得EF的长;
(2)运动过程中使△DEF为等腰三角形,则要考虑哪两边为腰,故要考虑三种情况,当DF=EF时,当DE=EF时,当DE=EF时.分别讨论易根据三角形相似、边成比例及(1)中EF的值得到关于t的方程,解得即可.
解答 解:(1)∵BD=tcm,DE=4cm,
∴BE=BD+DE=(t+4)cm,
∵EF∥AC,
∴△BEF∽△BCA,
∴EF:CA=BE:BC,
即EF:10=(t+4):16,
解得:EF=$\frac{5}{8}$(t+4)(cm);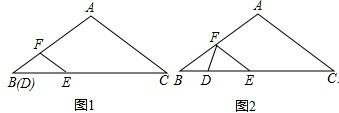 (2)分三种情况讨论:
(2)分三种情况讨论:
①如图1,∵当DF=EF时,
∴∠EDF=∠DEF,
∵AB=AC,
∴∠B=∠C,
∵EF∥AC,
∴∠DEF=∠C,
∴∠EDF=∠B,
∴点B与点D重合,
∴t=0;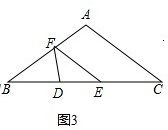 ②如图2,当DE=EF时,
②如图2,当DE=EF时,
则4=$\frac{5}{8}$(t+4),
解得:t=$\frac{12}{5}$;
③如图3,∵当DE=DF时,有∠DFE=∠DEF=∠B=∠C,
∴△DEF∽△ABC.
∴$\frac{DE}{AB}$=$\frac{EF}{BC}$,
即$\frac{4}{10}$=$\frac{\frac{5}{8}(t+4)}{16}$,
解得:t=$\frac{156}{25}$;
综上所述,当t=0、$\frac{12}{5}$或$\frac{156}{25}$秒时,△DEF为等腰三角形.
点评 此题考查了相似三角形的判定与性质、等腰三角形的判定与性质、三角形中位线的性质、平行四边形的性质以及矩形的判定与性质等知识.此题综合性很强,难度较大,注意掌握分类讨论思想、方程思想与数形结合思想的应用.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
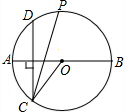 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )| A. | 到CD的距离保持不变 | B. | 到D点距离保持不变 | ||
| C. | 等分$\widehat{BD}$ | D. | 位置不变 |
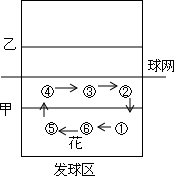 排球比赛中,甲、乙两方上场的各6名队员面对排球网,分别站在排球场的一边,6名队员一般站成两排,从排球场右下角开始,分别为1号位、2号位、3号位、4号位、5号位、6号位.
排球比赛中,甲、乙两方上场的各6名队员面对排球网,分别站在排球场的一边,6名队员一般站成两排,从排球场右下角开始,分别为1号位、2号位、3号位、4号位、5号位、6号位. 如图,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求证:∠BAD=∠CAE.
如图,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求证:∠BAD=∠CAE.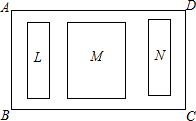 要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.
要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.