题目内容
14．
如图，$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$，求证：∠BAD=∠CAE．
分析 根据三边对应成比例，两三角形相似得到△ABC∽△ADE，根据相似三角形的性质即可得到结论．
解答 证明：∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAC-∠DAC，
即∠BAD=∠CAE．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
相关题目
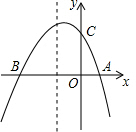如图，已知抛物线y=ax2+bx+c与x轴交于A（m，0），B（n，0），点A位于点B的右侧，且m、n是一元二次方程x2+2x-3=0的两个根，与y轴交于C（0，3）．点P在抛物线上，点Q在x轴上，是否存在以点P、Q、A、C为顶点的四边形是平行四边形？若存在，求出点P、Q的坐标；若不存在，请说明理由．
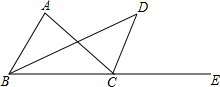如图所示，已知BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，且与BD交于点D；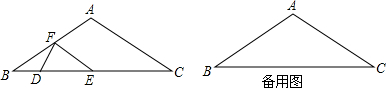
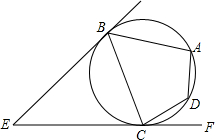如图，EB，EC是⊙O的两条切线，与⊙O相切于B，C两点，点A，D在圆上．若∠E=46°，∠DCF=32°，则∠A的度数是99°．