题目内容
18．
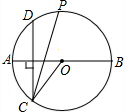如图，AB为⊙O的直径，作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在下半圆上移动时，（不与点A、B重合），下列关于点P描述正确的是（ ）| A． | 到CD的距离保持不变 | B． | 到D点距离保持不变 | ||
| C． | 等分$\widehat{BD}$ | D． | 位置不变 |
分析 首先连接OP，由∠OCD的平分线交⊙O于点P，易证得CD∥OP，又由弦CD⊥AB，可得OP⊥AB，即可证得点P为$\widehat{AB}$的中点不变．
解答 
解：不发生变化．
连接OP，
∵OP=OC，
∴∠P=∠OCP，
∵∠OCP=∠DCP，
∴∠P=∠DCP，
∴CD∥OP，
∵CD⊥AB，
∴OP⊥AB，
∴$\widehat{AP}$=$\widehat{BP}$，
∴点P为$\widehat{AB}$的中点不变．
故选D．
点评 此题考查了圆周角定理以及垂径定理，正确的作出辅助线是解题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
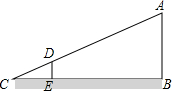如图，小亮欲测量一电线杆AB的高度，他站在该电线杆的影子上前后移动，直到他身体影子的顶端正好与电线杆影子的顶端重叠，此时同伴测出小亮与电线杆的距离BE=12m，小亮的影子长CE=4m，已知小亮的身高DE=1.7m．
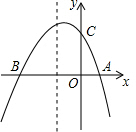如图，已知抛物线y=ax2+bx+c与x轴交于A（m，0），B（n，0），点A位于点B的右侧，且m、n是一元二次方程x2+2x-3=0的两个根，与y轴交于C（0，3）．点P在抛物线上，点Q在x轴上，是否存在以点P、Q、A、C为顶点的四边形是平行四边形？若存在，求出点P、Q的坐标；若不存在，请说明理由．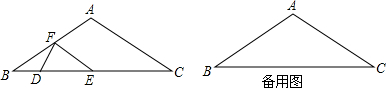
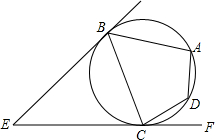如图，EB，EC是⊙O的两条切线，与⊙O相切于B，C两点，点A，D在圆上．若∠E=46°，∠DCF=32°，则∠A的度数是99°．
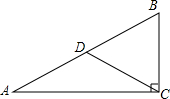已知，在Rt△ABC中，∠ACB=90°，CD是AB上的中线，⊙O经过A，C，D三点，BC的延长线交⊙O于点E．