题目内容
15.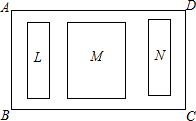 要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.
要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.
分析 把L、M、N合并成矩形得长为(60-4×硬化路面的宽),宽为(40-2×硬化路面的宽),由等量关系三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,列出方程解答即可.
解答 解:设L、M、N三块绿地周围的硬化路面的宽都为x米,
根据题意,得:(60-4x)×(40-2x)=60×40×$\frac{1}{2}$,
解得,x1=5,x2=30,
经检验,x2=30不符合题意,舍去.
答:三块绿地周围的硬化路面宽都为5米.
点评 此题考查一元二次方程的实际运用,根据题意找出等量关系列出方程解决问题.

练习册系列答案
相关题目
20.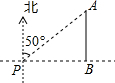 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
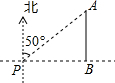 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )| A. | 10海里 | B. | 10sin50°海里 | C. | 10cos50°海里 | D. | 10tan50°海里 |
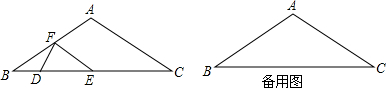
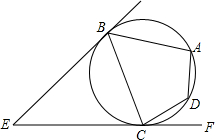 如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°.
如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°.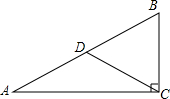 已知,在Rt△ABC中,∠ACB=90°,CD是AB上的中线,⊙O经过A,C,D三点,BC的延长线交⊙O于点E.
已知,在Rt△ABC中,∠ACB=90°,CD是AB上的中线,⊙O经过A,C,D三点,BC的延长线交⊙O于点E.