题目内容
已知四边形ABCD中,AB=CD,AD=BC,O为AC上一点,过点O的直线分别交直线AD、BC于点E、F.
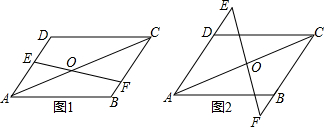
(1)如图1,若E、F分别在AD、BC上,求证:∠AEF=∠CFE;
(2)如图2,若E、F分别在AD、CB的延长线上,(1)中的结论是否成立?请画图并证明你的结论.

(1)如图1,若E、F分别在AD、BC上,求证:∠AEF=∠CFE;
(2)如图2,若E、F分别在AD、CB的延长线上,(1)中的结论是否成立?请画图并证明你的结论.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)欲证明∠AEF=∠CFE,只需证得AD∥BC即可,则需要证明四边形ABCD是平行四边形;
(2)解题思路同(1).
(2)解题思路同(1).
解答:证明: (1)如图1,∵四边形ABCD中,AB=CD,AD=BC,
(1)如图1,∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEF=∠CFE;
(2)(1)中的结论成立.理由如下:
如图2,∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
又∵E、F分别在AD、CB的延长线上,
∴AE∥CF,
∴∠AEF=∠CFE.
 (1)如图1,∵四边形ABCD中,AB=CD,AD=BC,
(1)如图1,∵四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEF=∠CFE;
(2)(1)中的结论成立.理由如下:
如图2,∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
又∵E、F分别在AD、CB的延长线上,
∴AE∥CF,
∴∠AEF=∠CFE.
点评:本题考查了平行四边形的判定与性质.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列条件中,能确定点A、B、C在同一条直线上的是( )
| A、AB=2,BC=5,AC=7 |
| B、AB=4,BC=3,AC=9 |
| C、AB=2,BC=11,AC=8 |
| D、AB=3,BC=6 AC=12 |
 如图,在四边形ABCD中,AB=AC,∠BAC+∠BDC=180°,CE∥DB交AD于E,探究线段EC与DC的数量关系.
如图,在四边形ABCD中,AB=AC,∠BAC+∠BDC=180°,CE∥DB交AD于E,探究线段EC与DC的数量关系.