题目内容
14.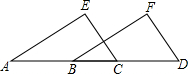 已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.
已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.
分析 首先利用平行线的性质得出,∠A=∠FBD,∠D=∠ECA,根据AB=CD即可得出AC=BD,进而得出△EAC≌△FBD.
解答  证明:∵EA∥FB,
证明:∵EA∥FB,
∴∠A=∠FBD,
∵EC∥FD,
∴∠D=∠ECA,
∵AB=CD,
∴AC=BD,
在△EAC和△FBD中,
$\left\{\begin{array}{l}{∠ECA=∠D}\\{∠A=∠FBD}\\{AC=BD}\end{array}\right.$,
∴△EAC≌△FBD(AAS),
∴EA=FB.
点评 此题主要考查了全等三角形的判定与性质等知识,解题时注意:两角及其夹边分别对应相等的两个三角形全等.根据已知得出△EAC≌△FBD是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下面的说法错误的是( )
| A. | 0是最小的整数 | B. | 1是最小的正整数 | ||
| C. | 0是最小的自然数 | D. | 自然数就是非负整数 |
19.(-15)+13的结果是( )
| A. | -2 | B. | 2 | C. | 28 | D. | -28 |
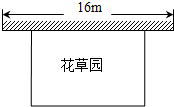 某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.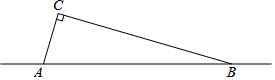 在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?
在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?