题目内容
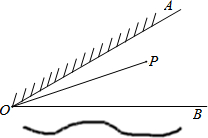 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.(1)请用尺规在图上画出此人行走的最短路线图(保留作图痕迹,不写作法和理由).
(2)若OP=30米,求此人行走的最短路线的长度.
考点:作图—应用与设计作图,轴对称-最短路线问题
专题:
分析:(1)利用轴对称最短路线求法得出P点关于OA,OB的对称点,进而得出行走路线;
(2)利用等边三角形的判定方法以及其性质得出此人行走的最短路线长为P′P″进而得出答案.
(2)利用等边三角形的判定方法以及其性质得出此人行走的最短路线长为P′P″进而得出答案.
解答: 解:(1)如图所示:此人行走的最短路线为:PC→CD→DP;
解:(1)如图所示:此人行走的最短路线为:PC→CD→DP;
(2)连接OP′,OP″,
由题意可得:OP′=OP″,∠P′OP″=60°,
则△P′OP″是等边三角形,
∵OP=30米,
∴PC+CD+DP=P′P″=30(m),
答;此人行走的最短路线的长度为30m.
 解:(1)如图所示:此人行走的最短路线为:PC→CD→DP;
解:(1)如图所示:此人行走的最短路线为:PC→CD→DP;(2)连接OP′,OP″,
由题意可得:OP′=OP″,∠P′OP″=60°,
则△P′OP″是等边三角形,
∵OP=30米,
∴PC+CD+DP=P′P″=30(m),
答;此人行走的最短路线的长度为30m.
点评:此题主要考查了利用轴对称求最值问题,得出最短行走路径是解题关键.

练习册系列答案
相关题目
点A在数轴上距原点5个单位长度,将A点先向左移动2个单位长度,再向右移动6个单位长度,此时A点所表示的数是( )
| A、-1 | B、9 |
| C、-1或9 | D、1或9 |
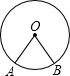 如图,A、B是⊙O上两点,且∠AOB=70°,点C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是( )
如图,A、B是⊙O上两点,且∠AOB=70°,点C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是( )| A、35° |
| B、145° |
| C、35°或145° |
| D、35°或110° |
 如图,线段AC是矩形ABCD的对角线,
如图,线段AC是矩形ABCD的对角线,