题目内容
已知:如图1,点M在x轴正半轴上,⊙M交坐标轴于A、B、C、D点,A(-1,0),C(0,
).

(1)求⊙M的半径;
(2)如图2,若点E为弧AC的中点,点D为弧EF的中点,在弧DF上有一动点P,连接DP,过点D作DQ⊥DP交PE于点Q连接QF,若N为PE的中点,试判断DN与QF的关系,并说明理由;
(3)如图3,点P为优弧CBD上一动点,连接PC、PA、PD,在PA上取点G使得GA=AC,求
的值.
| 3 |

(1)求⊙M的半径;
(2)如图2,若点E为弧AC的中点,点D为弧EF的中点,在弧DF上有一动点P,连接DP,过点D作DQ⊥DP交PE于点Q连接QF,若N为PE的中点,试判断DN与QF的关系,并说明理由;
(3)如图3,点P为优弧CBD上一动点,连接PC、PA、PD,在PA上取点G使得GA=AC,求
| PC+PD-CD |
| PG |
考点:圆的综合题,全等三角形的判定与性质,等腰三角形的判定,勾股定理,三角形中位线定理,垂径定理,圆心角、弧、弦的关系,圆周角定理,相似三角形的判定与性质,特殊角的三角函数值
专题:压轴题
分析:(1)由A(-1,0),C(0,
)可得OA=1,OC=
.设⊙M的半径为r,在Rt△COM中运用勾股定理就可求出⊙M的半径.
(2)连接ED并延长到点S,使得SD=ED,连接SP并延长交QF于点R,连接FE、FD、FP、FS、MC,如图2.先求出
的度数,然后根据条件可得到EF是⊙M的直径.可证到△EDF和△QDP都是等腰直角三角形,从而可以证到△EDQ≌△FDP,则有EQ=FP.根据三角形中位线定理可得DN∥PS,DN=
PS;DM∥FS,DM=
FS.进而可以得到EF=FS,∠PEF=∠PFS,从而可以证到△EQF≌△FPS,则有QF=PS,∠EFQ=∠FSP,进而可证到DN=
QF,SR⊥QF,然后由DN∥SR就可得到DN⊥QF.
(3)设AP与CD交于点K,连接DA、DP,如图3.根据勾股定理可求出AC长,由
=
可得AC=AD.易证△APC∽△ACK,从而可以得到PC=
,同理可得PD=
,进而可以得到PC+PD-CD=
PG,就可求出
的值.
| 3 |
| 3 |
(2)连接ED并延长到点S,使得SD=ED,连接SP并延长交QF于点R,连接FE、FD、FP、FS、MC,如图2.先求出
 |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)设AP与CD交于点K,连接DA、DP,如图3.根据勾股定理可求出AC长,由
 |
| AC |
 |
| AD |
| AP•CK |
| AC |
| AP•KD |
| AD |
| 3 |
| PC+PD-CD |
| PG |
解答: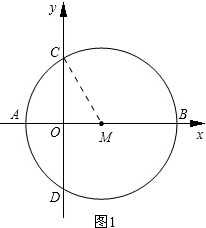 解:(1)连接MC,如图1.
解:(1)连接MC,如图1.
∵A(-1,0),C(0,
),
∴OA=1,OC=
.
设⊙M的半径为r,则有MA=MC=r.
∵∠COM=90°,
∴OM2+OC2=MC2.
∴(r-1)2+(
)2=r2.
解得:r=2.
∴⊙M的半径为2.
(2)DN=
QF,DN⊥QF.
证明:连接ED并延长到点S,使得SD=ED,连接SP并延长交QF于点R,
连接FE、FD、FP、FS、MC,如图2.
在Rt△COM中,
∵sin∠CMO=
=
,
∴∠CMO=60°.
∴
的度数为60°.
∵MA⊥CD,
∴
=
,
∴
的度数为60°.
∵点E为弧AC的中点,
∴
=
=
.
∴
的度数为30°.
∴
的度数为90°.
∵点D为弧EF的中点,
∴
=
.
∴
的度数为90°.
∴
的度数为180°.
∴EF是⊙M的直径.
∴∠EDF=90°.
∵
=
,∴DE=FD.
∵
的度数为90°,
∴∠DPE=45°.
∵DQ⊥DP,即∠QDP=90°,
∴∠DQP=90°-45°=45°=∠DPQ.
∴DQ=DP.
∵∠EDF=∠QDP=90°,
∴∠EDQ=∠FDP.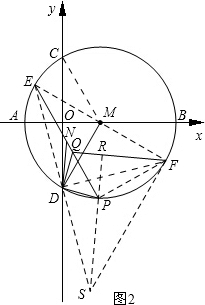
在△EDQ和△FDP中,
.
∴△EDQ≌△FDP.
∴EQ=FP.
∵N为PE的中点,ED=SD,
∴DN∥PS,DN=
PS.
∵DE=DS,ME=MF,
∴DM∥FS,DM=
FS.
∴∠EFS=∠EMD=90°,EF=FS.
∵EF是⊙M的直径,
∴∠EPF=90°.
∵∠EFS=∠EPF=90°,
∴∠PEF=90°-∠EFP=∠PFS.
在△EQF和△FPS中,
.
∴△EQF≌△FPS(SAS).
∴QF=PS,∠EFQ=∠FSP.
∴DN=
PS=
QF,∠FSP+∠RFS=∠EFQ+∠RFS=90°.
∴∠SRF=90°,即SR⊥QF.
∵DN∥PS,即DN∥SR,
∴DN⊥QF.
(3)设AP与CD交于点K,连接DA、DP,如图3.
∵∠AOC=90°,OA=1,OC=
,
∴AC=
=2.
∵
=
,
∴AC=AD=2.
∵
=
,
∴∠ACD=∠APC.
∵∠KAC=∠CAP,
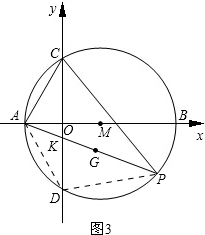 ∴△APC∽△ACK.
∴△APC∽△ACK.
∴
=
.
∴PC=
.
同理可得:PD=
.
∴PC+PD-CD
=
+
-CD
=
+
-2CO
=
-2
=
AP-2
=
(AG+PG)-2
=
(AC+PG)-2
=2
+
PG-2
=
PG.
∴
=
=
.
∴
的值为
.
 解:(1)连接MC,如图1.
解:(1)连接MC,如图1.∵A(-1,0),C(0,
| 3 |
∴OA=1,OC=
| 3 |
设⊙M的半径为r,则有MA=MC=r.
∵∠COM=90°,
∴OM2+OC2=MC2.
∴(r-1)2+(
| 3 |
解得:r=2.
∴⊙M的半径为2.
(2)DN=
| 1 |
| 2 |
证明:连接ED并延长到点S,使得SD=ED,连接SP并延长交QF于点R,
连接FE、FD、FP、FS、MC,如图2.
在Rt△COM中,
∵sin∠CMO=
| OC |
| CM |
| ||
| 2 |
∴∠CMO=60°.
∴
 |
| AC |
∵MA⊥CD,
∴
 |
| AC |
 |
| AD |
∴
 |
| AD |
∵点E为弧AC的中点,
∴
 |
| AE |
 |
| EC |
| 1 |
| 2 |
 |
| AC |
∴
 |
| AE |
∴
 |
| DE |
∵点D为弧EF的中点,
∴
 |
| DE |
 |
| FD |
∴
 |
| DF |
∴
 |
| EF |
∴EF是⊙M的直径.
∴∠EDF=90°.
∵
 |
| DE |
 |
| FD |
∵
 |
| DE |
∴∠DPE=45°.
∵DQ⊥DP,即∠QDP=90°,
∴∠DQP=90°-45°=45°=∠DPQ.
∴DQ=DP.
∵∠EDF=∠QDP=90°,
∴∠EDQ=∠FDP.

在△EDQ和△FDP中,
|
∴△EDQ≌△FDP.
∴EQ=FP.
∵N为PE的中点,ED=SD,
∴DN∥PS,DN=
| 1 |
| 2 |
∵DE=DS,ME=MF,
∴DM∥FS,DM=
| 1 |
| 2 |
∴∠EFS=∠EMD=90°,EF=FS.
∵EF是⊙M的直径,
∴∠EPF=90°.
∵∠EFS=∠EPF=90°,
∴∠PEF=90°-∠EFP=∠PFS.
在△EQF和△FPS中,
|
∴△EQF≌△FPS(SAS).
∴QF=PS,∠EFQ=∠FSP.
∴DN=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠SRF=90°,即SR⊥QF.
∵DN∥PS,即DN∥SR,
∴DN⊥QF.
(3)设AP与CD交于点K,连接DA、DP,如图3.
∵∠AOC=90°,OA=1,OC=
| 3 |
∴AC=
| OA2+OC2 |
∵
 |
| AC |
 |
| AD |
∴AC=AD=2.
∵
 |
| AC |
 |
| AD |
∴∠ACD=∠APC.
∵∠KAC=∠CAP,
 ∴△APC∽△ACK.
∴△APC∽△ACK.∴
| PC |
| CK |
| AP |
| AC |
∴PC=
| AP•CK |
| AC |
同理可得:PD=
| AP•KD |
| AD |
∴PC+PD-CD
=
| AP•CK |
| AC |
| AP•KD |
| AD |
=
| AP•CK |
| 2 |
| AP•KD |
| 2 |
=
| AP•CD |
| 2 |
| 3 |
=
| 3 |
| 3 |
=
| 3 |
| 3 |
=
| 3 |
| 3 |
=2
| 3 |
| 3 |
| 3 |
=
| 3 |
∴
| PC+PD-CD |
| PG |
| ||
| PG |
| 3 |
∴
| PC+PD-CD |
| PG |
| 3 |
点评:本题考查了圆弧与圆心角与弦的关系、圆周角定理、垂径定理、特殊角的三角函数值、全等三角形的判定与性质、相似三角形的判定与性质、三角形中位线定理、等腰三角形的判定、勾股定理等知识,综合性非常强,难度比较大.而证到△EDF和△QDP都是等腰直角三角形,从而证到△EDQ≌△FDP,进而证到△EQF≌△FPS是解决第(2)小题的关键;利用相似三角形的性质得到PC=
,PD=
是解决第(3)小题的关键.
| AP•CK |
| AC |
| AP•KD |
| AD |

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
下列各一元二次方程中两根之积为2的是( )
| A、x2-3x-1=0 |
| B、x2-x+2=0 |
| C、x2-3x-2=0 |
| D、x2-3x+2=0 |
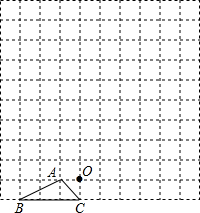 图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹. 如图,△ABC为等腰直角三角形,BC是斜边,AD∥BC,BD交AC于点E且BD=BC.求证:CE=CD.
如图,△ABC为等腰直角三角形,BC是斜边,AD∥BC,BD交AC于点E且BD=BC.求证:CE=CD.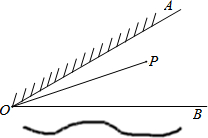 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里. 等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.
等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.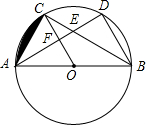 如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点.
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点.