题目内容
已知关于x的一元二次方程(2x+n)2=4x有两个非零不等实数根x1、x2,设m=
+
.
(1)求n的取值范围;
(2)试用关于n的代数式表示出m;
(3)是否存在这样的n值,使m的值等于1?若存在,求出这样的所有n的值;若不存在,请说明理由.
| 1 |
| x1 |
| 1 |
| x2 |
(1)求n的取值范围;
(2)试用关于n的代数式表示出m;
(3)是否存在这样的n值,使m的值等于1?若存在,求出这样的所有n的值;若不存在,请说明理由.
考点:根与系数的关系,根的判别式
专题:
分析:(1)由关于x的一元二次方程(2x+n)2=4x有两个非零不等实数根,即可得△=[4(n-1)]2-4×4n2>0且n2≠0,继而求得n的取值范围;
(2)由x1,x2是关于x的一元二次方程4x2+4(n-1)x+n2=0的两个实数根,根据根与系数的关系可得:x1+x2=-
=1-n,x1•x2=
,又由m=
+
,即可求得答案;
(3)当m=1时,即
=1,解此方程即可求得n的值,又由(1)中n的取值范围是n<
,且n≠0,即可求得n的值.
(2)由x1,x2是关于x的一元二次方程4x2+4(n-1)x+n2=0的两个实数根,根据根与系数的关系可得:x1+x2=-
| 4(n-1) |
| 4 |
| n2 |
| 4 |
| 1 |
| x1 |
| 1 |
| x2 |
(3)当m=1时,即
| 4(1-n) |
| n2 |
| 1 |
| 2 |
解答:解:(1)将方程整理得:4x2+4(n-1)x+n2=0,
∵方程有两个非零不等实数根,
∴△=[4(n-1)]2-4×4n2>0且n2≠0,
解得n<
,且n≠0
∴n的取值范围是n<
,且n≠0;
(2)∵x1,x2是关于x的一元二次方程4x2+4(n-1)x+n2=0的两个实数根,
∴x1+x2=-
=1-n,x1•x2=
,
∴m=
+
=
=
=
;
(3)存在.
理由:当m=1时,即
=1,
整理得:n2+4n-4=0,
解得:n=-2±2
,
∵n<
,
∴n=-2+2
不符合题意,舍去;
∴使m=1的值存在,此时n=-2-2
.
∵方程有两个非零不等实数根,
∴△=[4(n-1)]2-4×4n2>0且n2≠0,
解得n<
| 1 |
| 2 |
∴n的取值范围是n<
| 1 |
| 2 |
(2)∵x1,x2是关于x的一元二次方程4x2+4(n-1)x+n2=0的两个实数根,
∴x1+x2=-
| 4(n-1) |
| 4 |
| n2 |
| 4 |
∴m=
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 1-n | ||
|
| 4(1-n) |
| n2 |
(3)存在.
理由:当m=1时,即
| 4(1-n) |
| n2 |
整理得:n2+4n-4=0,
解得:n=-2±2
| 2 |
∵n<
| 1 |
| 2 |
∴n=-2+2
| 2 |
∴使m=1的值存在,此时n=-2-2
| 2 |
点评:此题考查了一元二次方程根与系数的关系、根的判别式的应用以及一元二次方程的解法.此题难度适中,注意掌握如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-
,x1x2=
的应用.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
下列计算中错误的是( )
A、a
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
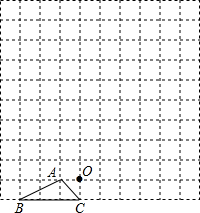 图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹. 如图,△ABC为等腰直角三角形,BC是斜边,AD∥BC,BD交AC于点E且BD=BC.求证:CE=CD.
如图,△ABC为等腰直角三角形,BC是斜边,AD∥BC,BD交AC于点E且BD=BC.求证:CE=CD.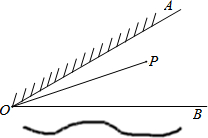 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里. 等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.
等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.