题目内容
14.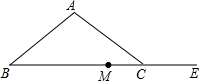 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.(1)尺规作图:作∠ABC的平分线,交AC于点D(保留作图痕迹,不写作法);
(2)E是底边BC的延长线上一点,M是BE的中点,连接DE、DM.若CE=CD,求证:DM⊥BE.
分析 (1)以点B为圆心,适当的长为半径作弧,交∠ABC于两点,分别以这两点为圆心,适当的长为半径画弧,交于一点,最后过该点与点B作射线,交AC于点D即可;
(2)先根据角平分线的定义以及三角形外角性质,求得∠E=∠DBC,进而得出BD=DE,再根据M是BE的中点即可得出结论.
解答 解:(1)如图所示,射线BD即为所求;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,
∴∠DBC=$\frac{1}{2}$∠ABC,
∵CD=CE,
∴∠E=∠CDE,
∵∠ACB是△CDE的外角,
∴∠E=$\frac{1}{2}$∠ACB,
∴∠E=∠DBC,
∴BD=DE,
又∵M是BE的中点,
∴DM⊥BE.
点评 本题主要考查了基本作图的运用以及等腰三角形的判定与性质的综合应用,解决问题的关键是掌握等腰三角形三线合一的性质.

练习册系列答案
相关题目
4.2017年元旦期间,某商场打出促销广告,如表所示.
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
| 优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
| 优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
6.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为( )
| A. | 50元、150元 | B. | 50元、100元 | C. | 100元、50元 | D. | 150元、50元 |
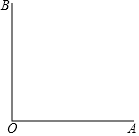 如图,已知∠AOB=90°,射线0A绕点O逆时针方向以毎秒6°的速度旋转(当旋转角度等于360°时,OA停止旋转),同时0B绕点O以每秒2°的速度旋转(当OA停止旋转时,OB同样 停止旋转).求当OA旋转多少秒,旋转后的OA与OB形成的角度为50°.
如图,已知∠AOB=90°,射线0A绕点O逆时针方向以毎秒6°的速度旋转(当旋转角度等于360°时,OA停止旋转),同时0B绕点O以每秒2°的速度旋转(当OA停止旋转时,OB同样 停止旋转).求当OA旋转多少秒,旋转后的OA与OB形成的角度为50°.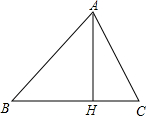 已知:如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D为AH上的一点,且DH=HC,连结BD并延长BD交AC于点E,连结EH.
已知:如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D为AH上的一点,且DH=HC,连结BD并延长BD交AC于点E,连结EH.