题目内容
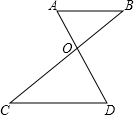 如图,已知AB∥CD,AD与BC相交于点O,且
如图,已知AB∥CD,AD与BC相交于点O,且| AB |
| CD |
| 2 |
| 3 |
(1)求
| AO |
| AD |
(2)如果
| AO |
| a |
| a |
| DA |
考点:*平面向量
专题:
分析:(1)由AB∥CD,可得△AOB∽△DOC,然后由相似三角形的对应边成比例,求得
的值.
(2)由(1)可得
=-
=-
.
| AO |
| AD |
(2)由(1)可得
| DA |
| 5 |
| 2 |
| AO |
| 5 |
| 2 |
| a |
解答:解:(1)∵AB∥CD,
∴△AOB∽△DOC,
∴
=
=
,
∴
=
;
(2)由(1)知,AD=
AO,
∴
=-
=-
.
∴△AOB∽△DOC,
∴
| AO |
| OD |
| AB |
| CD |
| 2 |
| 3 |
∴
| AO |
| AD |
| 2 |
| 5 |
(2)由(1)知,AD=
| 5 |
| 2 |
∴
| DA |
| 5 |
| 2 |
| AO |
| 5 |
| 2 |
| a |
点评:此题考查了平面向量的知识以及相似三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
一个扇形的圆心角为120°,半径为3,则这个扇形的面积为( )
| A、3π | B、9π | C、2π | D、4π |
在直角坐标系中,点M(1,-2012)关于原点的对称点坐标是( )
| A、(1,2012) |
| B、(-1,-2012) |
| C、(-1,2012) |
| D、(-2012,1) |
 如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为
如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为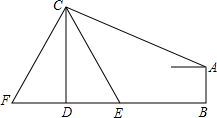 如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.
如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.