题目内容
参加一次足球联赛的每两队之间都要进行两次比赛，共要比赛90场，参加比赛的球队共有 个．
考点：一元二次方程的应用
专题：
分析：每个队都要与其余队比赛一场，2队之间要赛2场．等量关系为：队的个数×（队的个数-1）=90，把相关数值代入计算即可．
解答：解：设参加比赛的球队共有x个．
x（x-1）=90，
（x-10）（x+9）=0，
解得x=10，x=-9（不合题意，舍去）．
答：参加比赛的球队共有10个．
故答案为10．
x（x-1）=90，
（x-10）（x+9）=0，
解得x=10，x=-9（不合题意，舍去）．
答：参加比赛的球队共有10个．
故答案为10．
点评：本题考查一元二次方程的应用；得到比赛总场数的等量关系是解决本题的关键．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
如图，A、B两地之间有一座山，汽车原来从A地到B地须经C地沿折现A-C-B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=120千米，∠A=30°，∠B=135°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）．
已知△ABC∽△DEF，点A、B、C对应点分别是D、E、F，AB：DE=9：4，那么S△ABC：S△DEF等于（ ）
| A、3：2 | B、9：4 |
| C、16：81 | D、81：16 |
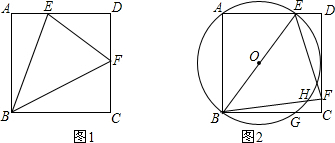
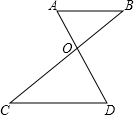如图，已知AB∥CD，AD与BC相交于点O，且