题目内容
16.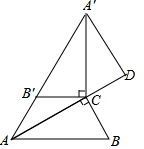 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 先根据,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,求得A′C=AC=3,再根据旋转的性质,求得∠A'CD=60°,最后在Rt△A'CD中,根据勾股定理即可得到A′D的长.
解答  解:∵∠ACB=90°,∠B=60°,
解:∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∵BC=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′C=AC=3,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴∠A'CD=60°,
又∵A′D∥BC,
∴∠D=∠BCD=90°,
∴Rt△A'CD中,CD=$\frac{1}{2}$A'C=$\frac{3}{2}$,
∴A'D=$\sqrt{A'{C}^{2}-C{D}^{2}}$=$\frac{3}{2}\sqrt{3}$,
故选:C.
点评 本题考查了旋转的性质,掌握对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等是本题的关键.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
7.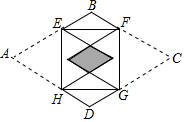 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )
 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( ) 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.