题目内容
6．为了鼓励学生课外阅读，学校公布了“阅读奖励”方案，并设置了“赞成、反对、无所谓”三种意见．现从学校所有2400名学生中随机征求了100名学生的意见，其中持“反对”和“无所谓”意见的共有30名学生，估计全校持“赞成”意见的学生人数约为（ ）| A． | 70 | B． | 720 | C． | 1680 | D． | 2370 |
分析 先求出100名学生中持“赞成”意见的学生人数，进而可得出结论．
解答 解：∵100名学生中持“反对”和“无所谓”意见的共有30名学生，
∴持“赞成”意见的学生人数=100-30=70名，
∴全校持“赞成”意见的学生人数约=2400×$\frac{70}{100}$=1680（名）．
故选C．
点评 本题考查的是用样本估计总体，先根据题意得出100名学生中持赞成”意见的学生人数是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．
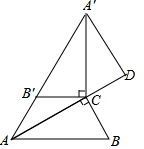如图，△ABC中，∠ACB=90°，∠B=60°，BC=$\sqrt{3}$，△A′B′C由△ABC绕C点顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，恰好A，B′，A′在同一条直线上，A′D∥BC交AC的延长线于点D，则A′D的长为（ ）
如图，△ABC中，∠ACB=90°，∠B=60°，BC=$\sqrt{3}$，△A′B′C由△ABC绕C点顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，恰好A，B′，A′在同一条直线上，A′D∥BC交AC的延长线于点D，则A′D的长为（ ）| A． | 3$\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
17．下列圆的内接正多边形中，一条边所对的圆心角最大的图形是（ ）
| A． | 正三角形 | B． | 正方形 | C． | 正五边形 | D． | 正六边形 |
14．如果一元二次方程2x2+3x+m=0有两个相等的实数根，那么实数m的取值为（ ）
| A． | m＞$\frac{9}{8}$ | B． | m$＞\frac{8}{9}$ | C． | m=$\frac{9}{8}$ | D． | m=$\frac{8}{9}$ |
1．
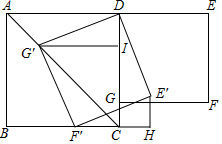如图，在正方形ABCD和正方形DEFG中，点G在CD上，DE=2，将正方形DEFG绕点D顺时针旋转60°，得到正方形DE′F′G′，此时点G′在AC上，连接CE′，则CE′+CG′=（ ）
如图，在正方形ABCD和正方形DEFG中，点G在CD上，DE=2，将正方形DEFG绕点D顺时针旋转60°，得到正方形DE′F′G′，此时点G′在AC上，连接CE′，则CE′+CG′=（ ）| A． | $\sqrt{2}$$+\sqrt{6}$ | B． | $\sqrt{3}+1$ | C． | $\sqrt{3}+\sqrt{2}$ | D． | $\sqrt{3}+\sqrt{6}$ |
11．将抛物线y=x2向右平移2个单位，再向上平移1个单位，所得抛物线相应的函数表达式是（ ）
| A． | y=（x+2）2+1 | B． | y=（x+2）2-1 | C． | y=（x-2）2+1 | D． | y=（x-2）2-1 |
，BC=2，求⊙O的半径．
B. 
C. 
D. 