题目内容
5. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
分析 (1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可;
解答 解:(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=$\sqrt{A{B}^{2}-A{N}^{2}}$=$4\sqrt{3}$,
∴B($4\sqrt{3}$,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=$\frac{1}{2}$NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.
点评 本题考查圆的切线的判定、坐标与图形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列运算正确的是( )
| A. | a2+a2=a4 | B. | a2•a3=a6 | C. | (-2a2)3=8a6 | D. | (ab)2=a2b2 |
16.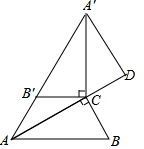 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
10.计算106×(102)3÷104的结果是( )
| A. | 103 | B. | 107 | C. | 108 | D. | 109 |
17.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
14.如果一元二次方程2x2+3x+m=0有两个相等的实数根,那么实数m的取值为( )
| A. | m>$\frac{9}{8}$ | B. | m$>\frac{8}{9}$ | C. | m=$\frac{9}{8}$ | D. | m=$\frac{8}{9}$ |

 B.
B.  C.
C.  D.
D. 