题目内容
解方程:
(1)2y2-100=0;
(2)(x+6)(x-6)=64.
(1)2y2-100=0;
(2)(x+6)(x-6)=64.
考点:解一元二次方程-直接开平方法
专题:
分析:(1)先移项,再直接开平方即可;
(2)根据平方差公式展开,再解方程即可.
(2)根据平方差公式展开,再解方程即可.
解答:解:(1)2y2=100,
y2=50,
y=±5
,
y1=5
,y2=-5
;
(2)去括号得,x2-36=64,
x2=100,
x=±10,
x1=10,x2=-10.
y2=50,
y=±5
| 2 |
y1=5
| 2 |
| 2 |
(2)去括号得,x2-36=64,
x2=100,
x=±10,
x1=10,x2=-10.
点评:本题考查了解一元二次方程,(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.

练习册系列答案
相关题目
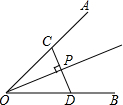 如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.| A、小于 | B、大于 |
| C、等于 | D、不能确定 |
下列方程中,不能用直接开平方法的是( )
| A、x2-3=0 |
| B、(x-1)2-4=0 |
| C、x2+2x=0 |
| D、(x-1)2=(2x+1)2 |
若x,y均为非负数,则方程2012x=-2013y的解的情况是( )
| A、无解 | B、有唯一解 |
| C、有无数解 | D、不能确定 |
 如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,
如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,