题目内容
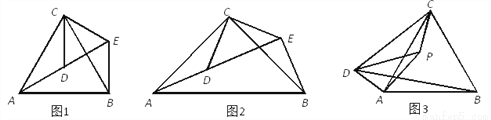
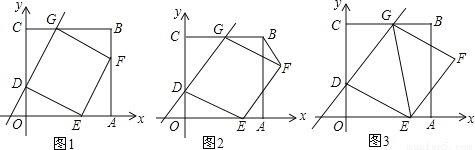
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则:
①∠BEC=_°;②线段AD、BE之间的数量关系是_.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
练习册系列答案
相关题目


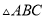 与
与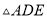 都是以
都是以 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, 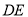 交
交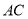 于点
于点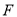 ,若
,若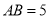 ,
, 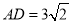 ,当
,当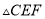 是直角三角形时,则
是直角三角形时,则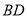 的长为__________.
的长为__________.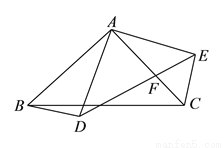
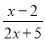 的值为0.
的值为0.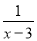 在实数范围内有意义,则实数x的取值范围是( )
在实数范围内有意义,则实数x的取值范围是( )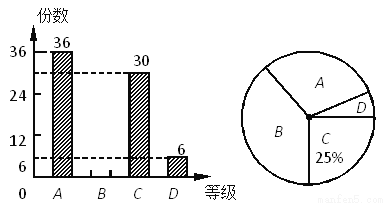
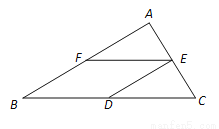
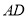 与通道
与通道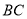 平行),通道水平宽度
平行),通道水平宽度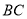 为8米,
为8米, 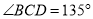 ,通道斜面
,通道斜面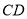 的长为6米,通道斜面
的长为6米,通道斜面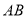 的坡度
的坡度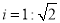 .
.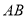 的长为 米;
的长为 米;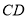 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面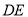 的坡角为30°,求此时
的坡角为30°,求此时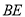 的长.(结果保留根号)
的长.(结果保留根号)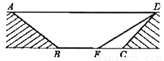
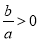 .其中正确的是( )
.其中正确的是( )