题目内容
4.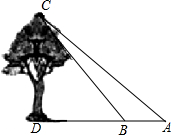 如图,从树顶C望地面上的AB两点,测得它们的俯角分别是45°和30°,已知AB=200m,点B在AD上,求树高CD.
如图,从树顶C望地面上的AB两点,测得它们的俯角分别是45°和30°,已知AB=200m,点B在AD上,求树高CD.
分析 由题意可知∠ECA=30°,∠ECB=45°,所以可证明△ABC是等腰三角形,所以AB=BC,解直角三角形BDC,进而求出建筑物CD的高.
解答 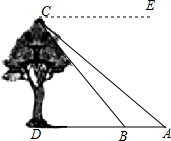 解:由题意可知∠ECA=30°,∠ECB=45°,
解:由题意可知∠ECA=30°,∠ECB=45°,
∴∠BAC=30°,∠DBC=45°,
∴BD=CD,
∵AD=$\frac{CD}{tan30°}$=$\sqrt{3}$CD,
∴AB=AD-BD=$\sqrt{3}$CD-CD=200,
∴CD=$\frac{200}{\sqrt{3}-1}$=100($\sqrt{3}$+1)m.
答:树高CD为100($\sqrt{3}$+1)m.
点评 本题考查了勾股定理的应用和解直角三角形的应用,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列条件不能判定两个直角三角形全等的是( )
| A. | 两条直角边对应相等 | B. | 有两条边对应相等 | ||
| C. | 一条边和一个锐角对应相等 | D. | 两个锐角对应相等 |
12.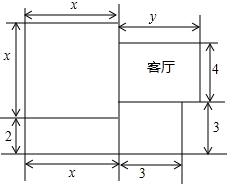 如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
(1)求y的值,并用含x的式子表示S;
(2)当x=5m时,求S;
(3)当S=x2+41时,求x.
 如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.(1)求y的值,并用含x的式子表示S;
(2)当x=5m时,求S;
(3)当S=x2+41时,求x.
13.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 4cm,5cm,13cm | C. | 5cm,7cm,11cm | D. | 4cm,4cm,9cm |
 如图,CD是Rt△ABC斜边上的高,则图中相等的锐角有2对.
如图,CD是Rt△ABC斜边上的高,则图中相等的锐角有2对.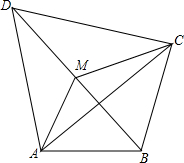 如图,已知四边形ABCD,M是BD的中点.
如图,已知四边形ABCD,M是BD的中点.