题目内容
3. 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若CD=2EF=6,BC=6$\sqrt{2}$,则∠C等于45°.
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若CD=2EF=6,BC=6$\sqrt{2}$,则∠C等于45°.
分析 连接BD,根据三角形中位线定理可得BD=2EF,再由条件CD=2EF可得BD=CD=6,再利用勾股定理逆定理证明∠BDC是90°,从而可得∠C的度数.
解答 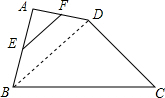 解:连接BD,
解:连接BD,
∵E、F分别是AB、AD的中点,
∴BD=2EF,
∵CD=2EF=6,
∴DB=6,
∵62+62=(6$\sqrt{2}$)2,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠C=$\frac{180°-90°}{2}$=45°.
故答案为:45.
点评 此题主要考查了三角形中位线定理,以及勾股定理逆定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半;如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
14.直线y=-x+3向上平移m个单位后,与直线y=-2x+4的交点在第一象限,则m的取值范围( )
| A. | -2<m<1 | B. | m>-1 | C. | -1<m<1 | D. | m<1 |
18.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数4相差2的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
 如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$.
如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$.
 如图,已知OC平分∠AOB,D是OC上任一点,⊙D与OA相切于点E,求证:OB与⊙D相切.
如图,已知OC平分∠AOB,D是OC上任一点,⊙D与OA相切于点E,求证:OB与⊙D相切. 如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°.
如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°.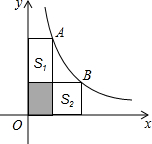 如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )