题目内容
20．已知x1、x2是一元二次方程x2-4x+1=0的两个根，则$\frac{1}{{x}_{1}}$+$\frac{1}{{{x}_{2}}}$等于（ ）| A． | -4 | B． | -1 | C． | 1 | D． | 4 |
分析 根据根与系数的关系可得x1+x2=4、x1•x2=1，将$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$通分后可得$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$，再代入x1+x2=4、x1•x2=1即可求出结论．
解答 解：∵x1、x2是一元二次方程x2-4x+1=0的两个根，
∴x1+x2=4，x1•x2=1，
$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{4}{1}$=4．
故选D．
点评 本题考查了根与系数的关系，根据根与系数的关系找出x1+x2=4、x1•x2=1是解题的关键．
练习册系列答案
相关题目
10．已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，则当x1＜x2＜2时，y1与y2的大小关系正确的是（ ）
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
| A． | y1≥y2 | B． | y1≤y2 | C． | y1＞y2 | D． | y1＜y2 |
8．在平面直角坐标系中，点A（3，-1）关于y轴的对称点A'的坐标是（ ）
| A． | （-3，-1） | B． | （3，1） | C． | （-3，1） | D． | （-1，3） |
15．在数轴上，表示数a的点到原点的距离是5个单位长度，数b是-$\frac{1}{3}$的倒数，则a+b=（ ）
| A． | 2或8 | B． | 2或-8 | C． | -2或8 | D． | -2或-8 |
5．
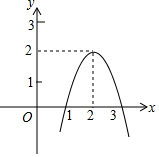已知二次函数y=ax2+bx+c （a≠0）的图象如图所示，当y＜0时，x的取值范围是（ ）
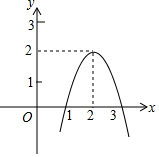已知二次函数y=ax2+bx+c （a≠0）的图象如图所示，当y＜0时，x的取值范围是（ ）| A． | 1＜x＜3 | B． | x＞3 | C． | 1＜x | D． | x＞3或x＜1 |
12．下列式子中是一元一次方程的是（ ）
| A． | $\frac{1}{x}$-2=5 | B． | 2x-3 | C． | x=y | D． | 3x=0 |
9．
若数字a的位置如图所示，化简|1+a|+|2-a|得（ ）
若数字a的位置如图所示，化简|1+a|+|2-a|得（ ）| A． | 1 | B． | -2a+1 | C． | 2a+1 | D． | 3 |