题目内容
 (1)如图,延长凸五边形A1A2A3A4A5的各边相交得到5个角,∠B1,∠B2,∠B3,∠B4,∠B5,求∠B1+∠B2+∠B3+∠B4+∠B5的度数;
(1)如图,延长凸五边形A1A2A3A4A5的各边相交得到5个角,∠B1,∠B2,∠B3,∠B4,∠B5,求∠B1+∠B2+∠B3+∠B4+∠B5的度数;(2)若延长凸n边形A1A2…An的各边得n个角,则得到n个角的和等于
考点:多边形内角与外角,三角形的外角性质
专题:
分析:(1)∠B1,∠B2,∠B3,∠B4,∠B5,它们可转移到一个三角形中,成为一个三角形的内角,故为180°;
(2)若延长凸n边形A1A2…An的各边得n个角,则得到的n个角的和等于:(n-2)•180°-n•180°+(n-2)•180°=(n-4)•180°.
(2)若延长凸n边形A1A2…An的各边得n个角,则得到的n个角的和等于:(n-2)•180°-n•180°+(n-2)•180°=(n-4)•180°.
解答: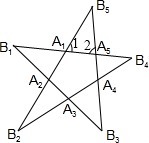 解:(1)如图,
解:(1)如图,
∵∠1=∠B2+∠B4,∠2=∠B1+∠B3,
∵∠1+∠2+∠B5=180°,
∴∠B1+∠B2+∠B3+∠B4+∠B5=180°;
(2)若延长凸n边形A1A2…An的各边得n个角,
则得到n个角的和=(n-2)•180°-n•180°+(n-2)•180°=(n-4)•180°.
故答案为(n-4)•180°.
 解:(1)如图,
解:(1)如图,∵∠1=∠B2+∠B4,∠2=∠B1+∠B3,
∵∠1+∠2+∠B5=180°,
∴∠B1+∠B2+∠B3+∠B4+∠B5=180°;
(2)若延长凸n边形A1A2…An的各边得n个角,
则得到n个角的和=(n-2)•180°-n•180°+(n-2)•180°=(n-4)•180°.
故答案为(n-4)•180°.
点评:本题考查三角形的外角性质以及多边形的内角和外角,关键是知道三角形的外角等于两个不相邻的内角的和以及多边形内角和的公式.

练习册系列答案
相关题目
下列说法中,正确的有( )
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,AB∥CD,AB=a,CD=b,则
如图,AB∥CD,AB=a,CD=b,则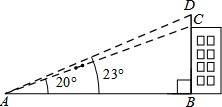 如图,大楼顶上有一根旗杆,杆高CD=3m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距BC的水平距离AB.
如图,大楼顶上有一根旗杆,杆高CD=3m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距BC的水平距离AB. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若AB=10,CD=8,则OP=
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若AB=10,CD=8,则OP= 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.BD=10,BE=8,BC=9,求△BCD的面积.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.BD=10,BE=8,BC=9,求△BCD的面积. 如图,AB为⊙O直径,∠BAC的平分线交⊙O于D点,∠BAC=50°,则∠ABD=
如图,AB为⊙O直径,∠BAC的平分线交⊙O于D点,∠BAC=50°,则∠ABD=