题目内容
4．
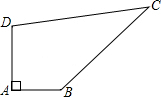如图，某开发区计划在一块四边形的空地ABCD上种植草坪，已知∠A=90°，AB=4m，BC=12m，CD=13m，DA=3m，种植每平方米草皮的预算费用为300元，若第一年对草坪的保养费用占种植草皮总预算的4%，以后每年的保养费用都将在前一年的基础上递增2%，求第三年的草坪保养费用．
分析 仔细分析题目，需要求得四边形的面积才能求得结果．连接BD，在直角三角形ABD中可求得BD的长，由BD、CD、BC的长度关系可得三角形DBC为一直角三角形，DC为斜边；由此看，四边形ABCD由Rt△ABD和Rt△DBC构成，则容易求解，再进一步得到第三年的草坪保养费用．
解答 
解：连接BD，
在Rt△ABD中，BD2=AB2+AD2=42+32=52，
在△CBD中，CD2=132，BC2=122，
而122+52=132，
即BD2+BC2=CD2，
∴∠DBC=90°，
S四边形ABCD=S△BAD+S△DBC=$\frac{1}{2}$×4×3+$\frac{1}{2}$×12×5=36．
所以需费用36×300×（4%+2%+2%）=864（元）．
答：第三年的草坪保养费用是864元．
点评 此题考查了勾股定理的应用，通过勾股定理由边与边的关系也可证明直角三角形，这样解题较为简单．
练习册系列答案
相关题目
12．在平面直角坐标系中，在第二象限的点是（ ）
| A． | （2，1） | B． | （2，-1） | C． | （-2，-1） | D． | （-2，1） |
如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（1，-2），B（3，-1），C（1，-1）．
9．
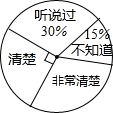第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施，为了了解居民对慈善法的知晓情况，某街道办从辖区居民中随机选取了900名居民进行调查，并将调查结果制作成了如下不完整的统计图和表：
根据以上信息求得“非常清楚”所占扇形的百分比为30%．
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施，为了了解居民对慈善法的知晓情况，某街道办从辖区居民中随机选取了900名居民进行调查，并将调查结果制作成了如下不完整的统计图和表：| 听说过 | 不知道 | 清楚 | 非常清楚 |
| A | B | 225 | C |
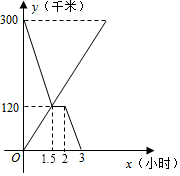甲、乙两车分别从A，B两地同时出发相向而行，并以各自的速度匀速行驶，甲车与乙车相遇后休息半小时，再按原速度继续前进到达B地；乙车从B地直接到达A地；两车到达各自目的地后即停止．如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．