题目内容
12．
如图，⊙O的直径AB垂直于弦CD，垂足为E，OC=10，OE=6，则CD的长是（ ）| A． | 8 | B． | 12 | C． | 16 | D． | 20 |
分析 根据垂径定理求出CD=2CE，根据勾股定理求出CE，即可得出答案．
解答 解：∵⊙O的直径AB垂直于弦CD，
∴CD=2CE，∠OEC=90°，
由勾股定理得：CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∴CD=2CE=16．
故选C．
点评 本题考查了勾股定理和垂径定理的应用，能求出CD=2CE是解此题的关键．
练习册系列答案
相关题目
20．
将长方形ABCD沿AE折叠，得到如图所示的图形，若∠CED′=56°，则∠D′AB的大小是（ ）
将长方形ABCD沿AE折叠，得到如图所示的图形，若∠CED′=56°，则∠D′AB的大小是（ ）| A． | 62° | B． | 28° | C． | 34° | D． | 56° |
已知二次函数y1=ax2+bx-3的图象经过点A（2，-3），B（-1，0），与y轴交于点C，与x轴另一交点交于点D．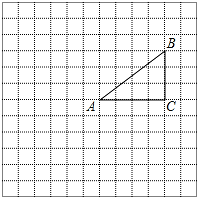
正方形网格中的每个小正方形的边长都是1，顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△A′B′C′．
如图，已知直线AB∥DE，∠ABC=80°，∠CDE=140°，求∠BCD的度数．