题目内容
13.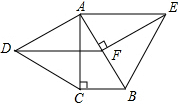 如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.
如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.(1)线段EF是多少?答:$\sqrt{3}$,请写出求解过程;
(2)请判断四边形ADFE的形状,并说明理由.
分析 (1)利用直角三角形中30°所对边与斜边的关系结合勾股定理得出答案;
(2)利用等边三角形的性质结合平行四边形的判定方法得出答案.
解答  解:(1)∵∠BAC=30°,BC=1,
解:(1)∵∠BAC=30°,BC=1,
∴AB=AE=BE=2,AC=$\sqrt{3}$,
∵△ABE是等边三角形,EF⊥AB,
∴AF=BF=1,
∴EF=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
(2)四边形ADFE是平行四边形,
理由:∵△ABD和△ACE都是等边三角形,
∴AD=BD=AB=2,AE=CE=AC=$\sqrt{3}$,∠ADB=∠BAD=∠DBA=∠CAE=∠AEC=∠ACE=60°,
∴∠DAB=∠EFA=90°,EF=AD=$\sqrt{3}$,
∴DA∥EF,
∴四边形ADFE是平行四边形.
点评 此题主要考查了等边三角形的性质以及平行四边形的判定等知识,得出AC,EF的长是解题关键.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | 2m3+3m2=5m5 | B. | -5(-x3)-2=-$\frac{5}{{x}^{6}}$ | C. | (3a3b3)2=6a6b6 | D. | $\sqrt{(-2)^{2}}$=-2 |
5.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需要( )张?


| A. | 15 | B. | 16 | C. | 21 | D. | 22 |
 如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.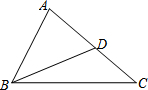 如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.
如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.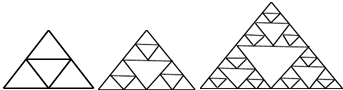
 解不等式3(x+1)-6≤4x,并把解集在数轴上表示出来.
解不等式3(x+1)-6≤4x,并把解集在数轴上表示出来.