题目内容
观察下列等式:39×41=402-12,48×52=502-22,56×64=602-42,65×75=702-52…,根据你发现的规律计算:1998×2002= .
考点:规律型:数字的变化类
专题:
分析:通过观察等式可知:40=(39+41)÷2,50=(48+52)÷2,60=(56+64)÷2…;1=(41-39)÷2,2=(52-48)÷2,4=(64-56)÷2…因此可知两个数相乘等于两个数和的一半的平方减去两个数差的一半的平方.然后利用上述规律计算1998×2002=(
)2-(
)2即可.
| 1998+2002 |
| 2 |
| 1998-2002 |
| 2 |
解答:解:通过观察等式可知:40=(39+41)÷2,50=(48+52)÷2,60=(56+64)÷2…;1=(41-39)÷2,2=(52-48)÷2,4=(64-56)÷2…因此可知两个数相乘等于两个数和的一半的平方减去两个数差的一半的平方.
∴1998×2002=(
)2-(
)2=20002-4=3999996.
故答案为:3999996.
∴1998×2002=(
| 1998+2002 |
| 2 |
| 1998-2002 |
| 2 |
故答案为:3999996.
点评:考查了规律型:数字的变化,本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目
| cosβ•tanβ |
| sinβ•cotβ |
| A、sinβ | B、cosβ |
| C、tanβ | D、cotβ |
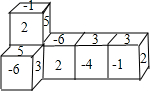 如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )
如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )| A、9 | B、8 | C、-15 | D、-13 |
下列说法不正确的是( )
A、
| ||||
| B、-9是81的算术平方根 | ||||
| C、(-0.1)2的平方根是±0.1 | ||||
D、
|
 如图,B,C,D是半径为6的⊙O上的三点,已知
如图,B,C,D是半径为6的⊙O上的三点,已知