题目内容
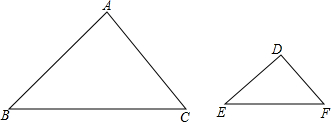 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为12
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为12| 5 |
考点:相似三角形的判定与性质
专题:
分析:证明△ABC∽△DEF,借助相似三角形的性质即可解决问题.
解答:解:∵AB=2DE,AC=2DF,
∴AB:DE=AC:DF=2,而∠A=∠D,
∴△ABC∽△DEF,
∴S△ABC:S△DEF=22=4,而 S△ABC=12
S△ABC=12
,
∴S△DEF=3
;
设EF边上的高为λ,
∵△ABC∽△DEF,
∴
=(
)2,
解得:λ=3,
即△DEF的边EF上的高和面积分别为3,3
.
∴AB:DE=AC:DF=2,而∠A=∠D,
∴△ABC∽△DEF,
∴S△ABC:S△DEF=22=4,而
 S△ABC=12
S△ABC=12| 5 |
∴S△DEF=3
| 5 |
设EF边上的高为λ,
∵△ABC∽△DEF,
∴
| S△ABC |
| S△DEF |
| 6 |
| λ |
解得:λ=3,
即△DEF的边EF上的高和面积分别为3,3
| 5 |
点评:该题主要考查了相似三角形的判定及其性质定理的应用问题;解题的关键是准确判断、深刻分析、灵活论证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
解方程:
(1)x2-4x-3=0;
(2)(x-3)2+2x(x-3)=0;
(3)2x2-10x=3;
(4)(x-5)(x+2)=8;
(5)3x2+5(2x+1)=0;
(6)2x2-7x-4=0.
(1)x2-4x-3=0;
(2)(x-3)2+2x(x-3)=0;
(3)2x2-10x=3;
(4)(x-5)(x+2)=8;
(5)3x2+5(2x+1)=0;
(6)2x2-7x-4=0.
若x、y为有理数,且|x-2|+(y+2)2=0,则(
)2013的值为( )
| x |
| y |
| A、2013 | B、-2013 |
| C、1 | D、-1 |
 如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.
如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.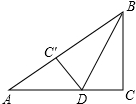 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )