题目内容
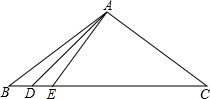 如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数.
如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数.考点:全等三角形的判定与性质
专题:
分析:延长BA到M,使AM=AE,易证△AEC≌△AMC,可得∠ACB=∠ACM,即可求得∠B和∠ACD的大小关系,根据三角形内角和为180°即可解题.
解答:解:延长BA到M,使AM=AE,
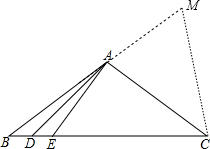
∵AC⊥AD,∠BAD=∠DAE=12°,
∴∠MAC=180°-∠BAD-∠CAD=90°-∠DAE=∠EAC,
在△AEC和△AMC中,
,
∴△AEC≌△AMC(SAS),
∴∠ACB=∠ACM,
∴∠M=∠BCM=2∠ACB,
∠ADC=90°-∠ACD=12°+∠B,
∴∠B=90°-12°-∠ACD=78°-∠ACD,
∵在△BMC中,∠B+∠M+∠BCM=180°,
∴4∠ACD+78°-∠ACD=180°,
∴∠ACD=34°.

∵AC⊥AD,∠BAD=∠DAE=12°,
∴∠MAC=180°-∠BAD-∠CAD=90°-∠DAE=∠EAC,
在△AEC和△AMC中,
|
∴△AEC≌△AMC(SAS),
∴∠ACB=∠ACM,
∴∠M=∠BCM=2∠ACB,
∠ADC=90°-∠ACD=12°+∠B,
∴∠B=90°-12°-∠ACD=78°-∠ACD,
∵在△BMC中,∠B+∠M+∠BCM=180°,
∴4∠ACD+78°-∠ACD=180°,
∴∠ACD=34°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△AEC≌△AMC是解题的关键.

练习册系列答案
相关题目
下列一元二次方程中,两实数根的和等于-4的是( )
| A、x2+2x-4=0 |
| B、x2-2x+4=0 |
| C、x2-4x-5=0 |
| D、x2+4x-5=0 |
 如图,能和∠α构成内错角的角的个数是( )
如图,能和∠α构成内错角的角的个数是( )| A、1 | B、2 | C、3 | D、4 |
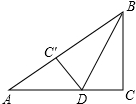 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )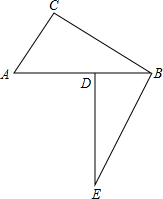 如图:AC⊥BC,ED⊥BD,BE⊥BC,垂足分别为C、D、B,AB=BE,试探究BE与AC+AD之间的关系.
如图:AC⊥BC,ED⊥BD,BE⊥BC,垂足分别为C、D、B,AB=BE,试探究BE与AC+AD之间的关系.