题目内容
15．
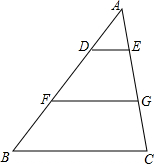如图，在△ABC中，DE∥BC，F，G分别为BD，CE的中点．已知BC=8，FG=5，则AD：FB等于（ ）| A． | 1：3 | B． | 2：3 | C． | 3：2 | D． | 3：1 |
分析 根据DE∥BC，于是得到$\frac{AD}{BD}=\frac{AE}{CE}$，由于F，G分别为BD，CE的中点，得到$\frac{AD}{DF}=\frac{AE}{EG}$，推出DE∥FG，得到DE∥FG∥BC，证得△AFG∽△ABC，根据相似三角形的性质即可得到结论．
解答 解：∵DE∥BC，
∴$\frac{AD}{BD}=\frac{AE}{CE}$，
∵F，G分别为BD，CE的中点，
∴$\frac{AD}{2DF}=\frac{AE}{2CE}$，
即$\frac{AD}{DF}=\frac{AE}{EG}$，
∴DE∥FG，
∴DE∥FG∥BC，
∴△AFG∽△ABC，
∴$\frac{AF}{AB}=\frac{FG}{BC}$=$\frac{5}{8}$，∴$\frac{AF}{BF}$=$\frac{5}{3}$，
∴AD：FB=2：3．
故选B．
点评 本题考查了相似三角形的判定和性质，平行线分线段成比例定理，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
相关题目
5．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{{a}^{2}-{b}^{2}}$ | B． | $\sqrt{20a}$ | C． | $\sqrt{{a}^{2}{b}^{4}}$ | D． | $\sqrt{\frac{1}{2a}}$ |
如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，则称这种走法为一次“移位”．如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的点，然后从1→2为第二次“移位”．小明从编号为4的点开始，第三次“移位”后，他到达编号为2的点，第2002次“移位”后，他到达编号为1的点．
如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E．∠DCA=40°，
7．如图是一个简单的数值运算程序，当输入的x的值为-1时，则输出的值为（ ）
| A． | 1 | B． | -5 | C． | -1 | D． | 5 |
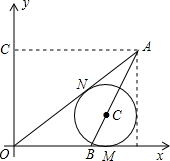如图，在直角坐标系中，点A的坐标是（8，6），点B的坐标是（5，0），点C在AB上，以C为圆心的圆与x轴相切，与AD切于点N，求⊙C的面积．