题目内容
6.如图1,在平面直角坐标系中,点A、B分别在x轴、y轴上.(1)如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点(点E不与点A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求证:AF=CE;
(2)如图2,若OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜想OP和MP的数量关系和位置关系,说明理由.
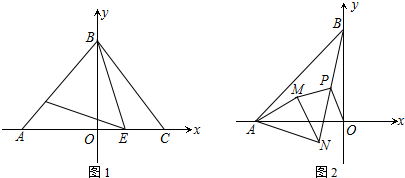
分析 (1)设∠OBE=α,∠AEF=β,证明∠EBC=∠AEF,EB=EF,进而可以证明△AEF和△CBE(AAS),利用全等三角形的对应边相等,即可解答;
(2)OP=MP且OP⊥MP,延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,证明△MPN≌△CPB(SAS),得到BC=MN=AM,∠MNP=∠CBP,再证明△MOC为等腰直角三角形,根据MP=CP,即可得到OP⊥MP且OP=MP.
解答 证明:(1)如图1,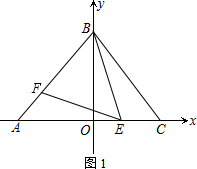
设∠OBE=α,∠AEF=β,
∴∠BAO=∠BEF=2α,
∵点A、C关于y轴对称,
∴BA=BC,
∴∠BAO=∠BCO=2α
∵∠AEB=2α+β=∠BCO+∠EBC
∴∠EBC=β,
即∠EBC=∠AEF
∵∠BFE=∠BAO+∠FEA=2α+β
又∠ABO=∠CBO=α+β
∴∠FBE=α+β+α=2α+β
∴∠BFE=∠FBE
∴EB=EF,
在△AEF和△CBE中$\left\{\begin{array}{l}∠AEF=∠CBE\\∠FAE=∠ECB\\ EF=BE\end{array}\right.$
∴△AEF≌△CBE(AAS)
∴AF=CE
(2)OP=MP且OP⊥MP,
理由如下:
延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,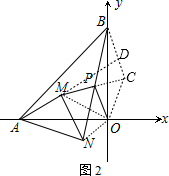
∵点P为BN的中点,
∴PN=PB,
在△MPN和△CPB中
$\left\{\begin{array}{l}MP=CP\\∠MPN=∠CPB\\ PN=PB\end{array}\right.$
∴△MPN≌△CPB(SAS)
∴BC=MN=AM,∠MNP=∠CBP,
∴MN∥BC,
∵∠AMN=90°
∴AD⊥BC,
∴∠MAO=∠CBO,
∴∠MOA=∠COB,MO=CO,
∴∠MOC=∠MOB+∠BOC=∠MOB+∠MOA=∠AOB=90°
∴△MOC为等腰直角三角形,
∵MP=CP,
∴OP⊥MP且OP=MP.
点评 本题考查了全等三角形的性质定理与判定定理,等腰三角形的性质、直角三角形的性质,解决本题的关键是作出辅助线,构建全等三角形.

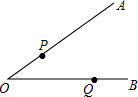 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )| A. | ∠AOB的平分线与PQ的交点 | |
| B. | ∠OPQ与∠OQP的角平分线的交点 | |
| C. | ∠AOB的平分线与线段PQ的垂直平分线的交点 | |
| D. | 线段PQ的垂直平分线与∠OPQ的平分线的交点 |
 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不能确定 |
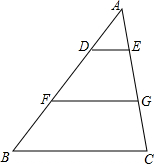 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )| A. | 1:3 | B. | 2:3 | C. | 3:2 | D. | 3:1 |
| A. | 重合 | B. | 平行或重合 | C. | 垂直 | D. | 相交但不垂直 |