题目内容
5.已知在直角坐标系中,A(1,0),B(-1,0),△ABC为等边三角形,则点C的坐标是(0,$\sqrt{3}$)或(0,-$\sqrt{3}$).分析 根据已知条件画出草图结合等边三角形的性质分析C点的可能位置,分情况求解.
解答  解:∵AB=2,以点A为圆心,2为半径画弧,交y轴于点C1,C2,
解:∵AB=2,以点A为圆心,2为半径画弧,交y轴于点C1,C2,
在直角三角形AC1O和直角三角形AC2O中,解直角三角形得C1O=C2O=$\sqrt{3}$,
∴C(0,$\sqrt{3}$)或(0,-$\sqrt{3}$).
故答案为(0,$\sqrt{3}$)或(0,-$\sqrt{3}$).
点评 本题考查了坐标与图形的性质及等边三角形的性质;解题时先运用画弧法确定点C的位置,再解直角三角形,求有关线段的长度,从而确定C点的坐标.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
15.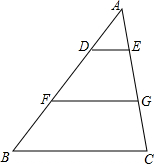 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )| A. | 1:3 | B. | 2:3 | C. | 3:2 | D. | 3:1 |
16.在同一平面内有1998条直线a1,a2,…,a1998,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…那么a1与a1998的位置关系是( )
| A. | 重合 | B. | 平行或重合 | C. | 垂直 | D. | 相交但不垂直 |
