题目内容
15.若关于x的一元二次方程x2+(a2-1)x+a-2=0有一根大于1,一根小于-1.求a的取值范围.分析 根据抛物线与x轴的交点问题,把一元二次方程x2+(a2-1)x+a-2=0有一根大于1,一根小于-1理解为抛物线y=x2+(a2-1)x+a-2与x轴的交点一个在点(-1,0)的左边,另一个交点在点(1,0)的右边,则利用函数图象得a-2<0;当x=-1时,y<0,即1-a2+1+a-2<0,当x=1时,y<0,即1+a2-1+a-2<0,然后求出三个不等式的公共部分即可.
解答 解:∵关于x的一元二次方程x2+(a2-1)x+a-2=0有一根大于1,一根小于-1,
∴抛物线y=x2+(a2-1)x+a-2与x轴的交点一个在点(-1,0)的左边,另一个交点在点(1,0)的右边,
∴a-2<0,即a<2,
∵抛物线开口向上,
∴当x=-1时,y<0,即1-a2+1+a-2<0,解得a<0或a>1,
当x=1时,y<0,即1+a2-1+a-2<0,解得-2<a<1,
∴-2<a<0.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程的问题.

练习册系列答案
相关题目
20.下列各式中,不能用平方差公式的是( )
| A. | (4x-3y)(3y-4x) | B. | (-4x+3y)(4x+3y) | C. | (-4x+3y)(-4x-3y) | D. | (4x+3y)(4x-3y) |
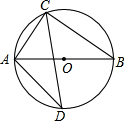 己知:在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,
己知:在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,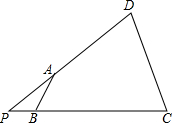 如图,四边形ABCD中,∠ABC=∠DCB,DA,CB的延长线交于点P.
如图,四边形ABCD中,∠ABC=∠DCB,DA,CB的延长线交于点P. 已知二次函数y=$\frac{1}{2}$x2+3x+2的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求四边形ACBD的面积.
已知二次函数y=$\frac{1}{2}$x2+3x+2的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求四边形ACBD的面积.