题目内容
若二次函数y=(k-2)x2-
x+k-5的图象与x轴只有一个交点,则k的值为 .
| 7 |
考点:抛物线与x轴的交点,二次函数的定义
专题:计算题
分析:根据二次函数的定义和抛物线与x轴的交点问题得到k-2≠0且△=(-
)2-4(k-2)(k-5)=0,然后解关于k的一元二次方程即可.
| 7 |
解答:解:根据题意得k-2≠0且△=(-
)2-4(k-2)(k-5)=0,
解得k1=
,k2=
,
所以k的值为
或
.
故答案为
或
.
| 7 |
解得k1=
| 11 |
| 2 |
| 3 |
| 2 |
所以k的值为
| 11 |
| 2 |
| 3 |
| 2 |
故答案为
| 11 |
| 2 |
| 3 |
| 2 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.注意考虑二次项系数不为0.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )
如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )| A、45° | B、55° |
| C、60° | D、75° |
下列说法中,正确的是( )
| A、无理数都是无限小数 | ||
| B、带根号的数都是无理数 | ||
C、
| ||
| D、9的平方根是3 |
比较大小:-3
( )-2
.
| 2 |
| 3 |
| A、> | B、< | C、= | D、不确定 |
下列图标是节水、节能、低碳和绿色食品的标志,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
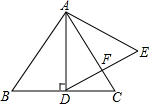 如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.
如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.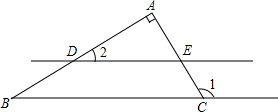 如图,∠1是△ABC的一个外角,∠A=90°,直线DE∥BC,分别交AB,AC于点D,E,∠1=120°,求∠2的度数.
如图,∠1是△ABC的一个外角,∠A=90°,直线DE∥BC,分别交AB,AC于点D,E,∠1=120°,求∠2的度数.