题目内容
当x=1时，px3+qx+6值为2010，则当x=-1时，px3+qx+6值为 ．
考点：代数式求值
专题：
分析：把x=1代入px2+qx+6可求得p+q的值，再代入要求的代数式可求得结果．
解答：解：由当x=1时，px3+qx+6值为2010，可得p+q+6=2010，所以p+q=2004，
当x=-1时，px3+qx+6=-p-q+6=-（p+q）+6=-2004+6=-1998，
故答案为：-1998．
当x=-1时，px3+qx+6=-p-q+6=-（p+q）+6=-2004+6=-1998，
故答案为：-1998．
点评：本题主要考查整体代入法求代数的值，由条件求得p+q的值代入是解题的关键．
练习册系列答案
相关题目
若关于x的一元二次方程（m+3）x2+2x+m2-9=0的常数项是0，则m的值等于（ ）
| A、3 | B、-3 | C、±3 | D、±9 |
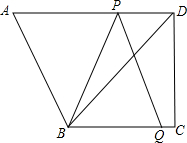在直角梯形ABCD中，AD∥BC，∠C=90度，BC=16，AD=21，DC=12，动点P从点D出发，沿线段DA方向以每秒2个单位长度的速度运动，动点Q从点C出发，在线段CB以每秒1个单位长度的速度向点B运动．点P、Q同时出发，当点P运动到点A时，点Q随之停止运动，设运动时间为t秒．
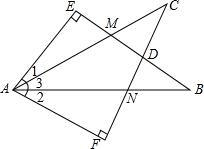如图，已知在△ABE和△ACF中，∠E=∠F=90°，AB=AC，BE=CF．
如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠BPD的度数为（ ）| A、45° | B、55° |
| C、60° | D、75° |