Question

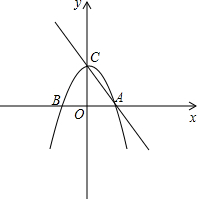已知抛物线y=-

1

2

x²+m-3与x轴交于A、B两点，且OA=OC．
（1）求m的值和抛物线的解析式；
（2）是否在抛物线上存在一点M，使S_△MAC=S_△OAC；
（3）是否在抛物线上存在一点M，使S_△MAB=S_△ABC；
（4）是否在直线AC线上存在一点M，使MB+MO的距离最短；
（5）是否在抛物线上存在一点M，使MC=MA；
（6）是否在抛物线上存在一点M，使△MAC是直角三角形．

Answer 1

考点：抛物线与x轴的交点

专题：

分析：（1）令x=0求出y的值得到OC的长度，然后表示出OA，再根据OA=OC列出方程求出m的值，即可得到抛物线解析式；
（2）根据等底等高的三角形的面积相等，过点O与AC平行的直线与抛物线的交点即为所求的点M；
（3）根据等底等高的三角形的面积相等，抛物线上到AB的距离等于点C到AB的距离的点即为所求的点M，然后根据点M的纵坐标利用抛物线解析式计算即可得解；
（4）根据轴对称确定最短路线问题，点O关于直线AC的对称点与点B的连线和AC的交点即为所求的点M；
（5）根据线段垂直平分线上的点到两端点的距离相等可得AC的垂直平分线与抛物线的交点即为所求的点M；
（6）先求出∠OCA=45°，再根据抛物线的对称性可知∠OCB=45°，然后求出∠ACB=90°，从而确定出点M、B重合时，△MAC是直角三角形；AM⊥AC时，求出AM的解析式，与抛物线解析式联立求解即可．

解答：解：（1）令x=0，则y=m-3，
所以，OC=m-3，
令y=0，则x²=2（m-3），
∵OA=OC，
∴2（m-3）=（m-3）²，
解得m₁=5，m₂=3（舍去），
∴抛物线为y=-

1

2

x²+2；

（2）∵m=5，OA=OC，
∴A（2，0），C（0，2），
∴直线AC的解析式为y=-x+2，
∵S_△MAC=S_△OAC，
∴点M到AC的距离等于点O到AC的距离，
联立

y=- 1 2 x2+2 y=-x

，
解得

x1=1+ 5 y1=-1- 5

，

x2=1- 5 y2=-1+ 5

，
∴存在点M（1+

5

，-1-

5

）或（1-

5

，-1+

5

），使S_△MAC=S_△OAC；

（3）∵S_△MAB=S_△ABC，
∴点M到AB的距离等于点C到AB的距离，
∴点M的纵坐标为-2，
∴-

1

2

x²+2=-2，
解得x=±2

2

，
∴点M的坐标为（-2

2

，-2）或（2

2

，-2）；

（4）∵点O关于直线AC：y=-x+2的对称点为O′（2，2），
∴直线BO′的解析式为y=

1

2

x+1，
联立

y= 1 2 x+1 y=-x+2

，
解得

x= 2 3 y= 4 3

，
∴点M的坐标为（

2

3

，

4

3

）；

（5）∵MC=MA，
∴点M在AC的垂直平分线上，
联立

y=x y=- 1 2 x2+2

，
解得

x1=-1+ 5 y1=-1+ 5

，

x2=-1- 5 y2=-1- 5

，
∴点M的坐标为（-1+

5

，-1+

5

）或（-1-

5

，-1-

5

）；

（6）∵OA=OC，
∴∠OCA=45°，
由抛物线的对称性可知∠OCB=45°，
∴∠ACB=90°，
∴点M与点B重合时，即M（-2，0）时，△MAC是直角三角形，
AM⊥AC时，直线AM的解析式为y=x-2，
联立

y=x-2 y=- 1 2 x2+2

，
解得

x1=2 y1=0

（为点A坐标），

x2=-4 y2=-6

，
∴点M的坐标为（-4，-6），
综上所述，存在点M（-2，0），（-4，-6），使△MAC是直角三角形．

点评：本题考查了抛物线与x轴的交点问题，等底等高的三角形的面积相等，线段垂直平分线上的点到两端点的距离相等的性质，等腰三角形的性质，联立两函数解析式求交点坐标．