题目内容
已知△ABC的三边分别为a、b、c,它们所对的角分别为A,B,C,若∠A=2∠B,b=4,c=5,则a= .
考点:正弦定理与余弦定理,等腰三角形的性质,相似三角形的判定与性质
专题:计算题
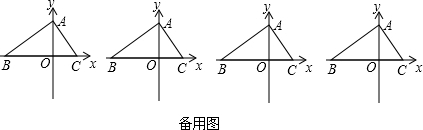
分析:方法一:如图1,利用正弦定理
=
和条件∠A=2∠B可得
=
,然后利用二倍角公式sin2B=2sinB•cosB可得cosB=
,结合余弦定理cosB=
可得
=
,然后把b=4,c=5代入等式就可求出a的值.
方法2:延长CA到点D,使得AD=AB,连接BD,如图2.根据等腰三角形的性质和三角形的外角性质可得∠CAB=2∠D,结合条件∠CAB=2∠ABC可得∠ABC=∠D,从而证到△CAB∽△CBD,然后运用相似三角形的性质就可解决问题.
| a |
| sinA |
| b |
| sinB |
| a |
| sin2B |
| b |
| sinB |
| a |
| 2b |
| a2+c2-b2 |
| 2ac |
| a |
| 2b |
| a2+c2-b2 |
| 2ac |
方法2:延长CA到点D,使得AD=AB,连接BD,如图2.根据等腰三角形的性质和三角形的外角性质可得∠CAB=2∠D,结合条件∠CAB=2∠ABC可得∠ABC=∠D,从而证到△CAB∽△CBD,然后运用相似三角形的性质就可解决问题.
解答:解:方法一:如图1,

根据正弦定理可得
=
.
∵∠A=2∠B,
∴
=
.
∵sin2B=2sinB•cosB,
∴
=
,
∴cosB=
.
根据余弦定理可得:cosB=
,
∴
=
,
∴b=4,c=5,
∴
=
,
整理得:a2=36,
∵a>0,∴a=6.
故答案为:6.
方法2:延长CA到点D,使得AD=AB,连接BD,如图2.

∵AD=AB,∴∠D=∠ABD.
∴∠CAB=∠D+∠ABD=2∠D.
∵∠CAB=2∠ABC,
∴∠ABC=∠D.
∵∠C=∠C,
∴△CAB∽△CBD,
∴
=
,
∴BC2=CA•CD.
∵AC=b=4,CD=CA+AD=CA+AB=b+c=4+5=9,BC=a,
∴a2=4×9=36.
∵a>0,∴a=6.
故答案为:6.

根据正弦定理可得
| a |
| sinA |
| b |
| sinB |
∵∠A=2∠B,
∴
| a |
| sin2B |
| b |
| sinB |
∵sin2B=2sinB•cosB,
∴
| a |
| 2sinB•cosB |
| b |
| sinB |
∴cosB=
| a |
| 2b |
根据余弦定理可得:cosB=
| a2+c2-b2 |
| 2ac |
∴
| a |
| 2b |
| a2+c2-b2 |
| 2ac |
∴b=4,c=5,
∴
| a |
| 8 |
| a2+25-16 |
| 10a |
整理得:a2=36,
∵a>0,∴a=6.
故答案为:6.
方法2:延长CA到点D,使得AD=AB,连接BD,如图2.

∵AD=AB,∴∠D=∠ABD.
∴∠CAB=∠D+∠ABD=2∠D.
∵∠CAB=2∠ABC,
∴∠ABC=∠D.
∵∠C=∠C,
∴△CAB∽△CBD,
∴
| BC |
| DC |
| CA |
| CB |
∴BC2=CA•CD.
∵AC=b=4,CD=CA+AD=CA+AB=b+c=4+5=9,BC=a,
∴a2=4×9=36.
∵a>0,∴a=6.
故答案为:6.
点评:本题考查了正弦定理、余弦定理、二倍角公式、相似三角形的判定与性质、等腰三角形的性质、三角形的外角性质等知识,由一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个正n边形的每个外角均为40°,则n=( )
| A、6 | B、7 | C、8 | D、9 |
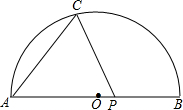 如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过
如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过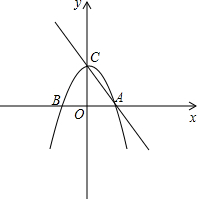 已知抛物线y=-
已知抛物线y=- 如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.
如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.