题目内容
已知：如图，将三个全等的正方形拼成一个矩形ABGH．求证：∠1+∠2=45°．考点：相似三角形的判定与性质
专题：证明题
分析：根据勾股定理可求出AB的长，再根据相似三角形的判定方法即可证明△ABC与△DBA相似；根据相似三角形的性质可得∠2=∠DBE，根据三角形的外角和定理即可求出∠1+∠2的度数．
解答：（1）证明：∵边长为a的三个正方形拼成一个矩形ABGH，
∴BD=
=
a，
∵DE=a，DH=2a，
∴
=
，
∵∠BDH=∠HDB，
∴△BDE∽△HDB；
∴∠2=∠DBE，
∵∠ADB=∠1+∠DBE=45°，
∴∠1+∠2=45°．
∴BD=
| AB2+AD2 |
| 2 |
∵DE=a，DH=2a，
∴
| BD |
| DH |
| DE |
| BD |
∵∠BDH=∠HDB，
∴△BDE∽△HDB；
∴∠2=∠DBE，
∵∠ADB=∠1+∠DBE=45°，
∴∠1+∠2=45°．
点评：本题考查了矩形的性质、勾股定理的运用、相似三角形的判定和性质以及三角形外角和定理，题目的综合性较强，难度一般．
练习册系列答案
相关题目
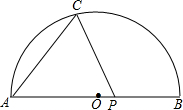如图，AB为半圆的直径，AB=10，点O到弦AC的距离为4，点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动，连接CP，经过
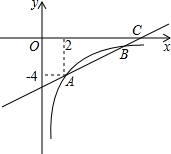如图，一次函数y=kx+b的图象交反比例函数y=
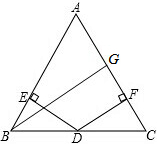如图，△ABC中，AB=AC，D在BC上（D不在BC中点），DE⊥AB于E，DF⊥AC于F，BG⊥AC于G，求证：DE+DF=BG．
已知抛物线y=-