题目内容
已知点P(a,4)在抛物线y=
x2+c和直线y=-2x上.
(1)求a,c的值;
(2)把此二次函数的图象沿着y轴方向平移,经过怎样的平移才能使所得的图象与直线y=-2x有且只有一个公共点?请说明理由.
| 1 |
| 4 |
(1)求a,c的值;
(2)把此二次函数的图象沿着y轴方向平移,经过怎样的平移才能使所得的图象与直线y=-2x有且只有一个公共点?请说明理由.
考点:二次函数的性质,二次函数图象与几何变换
专题:
分析:(1)首先将点P代入直线的解析式求得a的值,然后代入二次函数的解析式即可求得c值;
(2)设抛物线yy=
x2+3向上平移k个单位长度后得y-k=y=
x2+3则得方程-2x-k=y=
x2+3,得到△=82-4(4k+12)=16-16k,然后令16-16k=0,解得:k=1,从而确定平移的方向和单位.
(2)设抛物线yy=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)∵点P(a,4)在直线y=-2x上,
∴4=-2a,
即:a=-2,
又∵点P(-2,4)在抛物线y=
x2+c上,
∴4=
×(-2)2+c,
即:c=3;
(2)把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
理由:由(1)知,抛物线y=
x2+3和直线y=-2x有两个公共点,
因此设抛物线yy=
x2+3向上平移k个单位长度后得y-k=y=
x2+3,
则得方程-2x-k=y=
x2+3,
即:x2+8x+4k+12=0,
△=82-4(4k+12)=16-16k,
令16-16k=0,解得:k=1,
故把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
∴4=-2a,
即:a=-2,
又∵点P(-2,4)在抛物线y=
| 1 |
| 4 |
∴4=
| 1 |
| 4 |
即:c=3;
(2)把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
理由:由(1)知,抛物线y=
| 1 |
| 4 |
因此设抛物线yy=
| 1 |
| 4 |
| 1 |
| 4 |
则得方程-2x-k=y=
| 1 |
| 4 |
即:x2+8x+4k+12=0,
△=82-4(4k+12)=16-16k,
令16-16k=0,解得:k=1,
故把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
点评:本题考查了二次函数的性质及二次函数的图象与几何变换的知识,解题的关键是确定二次函数的解析式,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个正n边形的每个外角均为40°,则n=( )
| A、6 | B、7 | C、8 | D、9 |
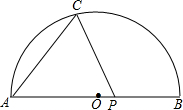 如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过
如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过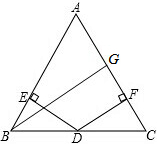 如图,△ABC中,AB=AC,D在BC上(D不在BC中点),DE⊥AB于E,DF⊥AC于F,BG⊥AC于G,求证:DE+DF=BG.
如图,△ABC中,AB=AC,D在BC上(D不在BC中点),DE⊥AB于E,DF⊥AC于F,BG⊥AC于G,求证:DE+DF=BG. 如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?
如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?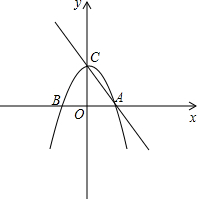 已知抛物线y=-
已知抛物线y=-