题目内容
平面直角坐标系中,以点P(2,a)为圆心的⊙P与y轴相切,直线y=x与⊙P相交于点A、B,且AB的长为2
,则a的值为 .
| 3 |
考点:圆的综合题,等腰三角形的性质,勾股定理,矩形的判定与性质,垂径定理,切线的性质,特殊角的三角函数值
专题:计算题
分析:设⊙P与y轴相切于点C,连接PC,则有PC⊥OC,根据点P的坐标可得⊙P的半径PC为2,由于满足条件的点P可能在直线y=x的上方,也可能在直线y=x的下方,因此需分两种情况讨论.当点P在直线y=x上方时,如图1,连接CP并延长交直线y=x于点E,则有CE=OC.过点P作PD⊥AB于D,由垂径定理可求出AD,在Rt△ADP中,运用勾股定理可求出PD,在Rt△PDE中,运用三角函数可求出PE,就可求出a的值;当点P在直线y=x下方时,如图2,连接PC,过点P作PD⊥AB于D,过点P作x轴的垂线交x轴与点M,交AB于点N,
同理可得:OM=MN,PD=1,PN=
.易证四边形PCOM是矩形,从而有OM=PC=2,OC=PM,进而可以求出a的值,问题得以解决.
同理可得:OM=MN,PD=1,PN=
| 2 |
解答:解: 设⊙P与y轴相切于点C,连接PC,则有PC⊥OC.
设⊙P与y轴相切于点C,连接PC,则有PC⊥OC.
∵点P的坐标为(2,a),∴PC=2.
①若点P在直线y=x上方,如图1,
连接CP并延长交直线y=x于点E,则有CE=OC.
∵CE⊥OC,CE=OC,
∴∠COE=∠CEO=45°.
过点P作PD⊥AB于D,
由垂径定理可得:AD=BD=
AB=
×2
=
.
在Rt△ADP中,
PD=
=
=1.
在Rt△PDE中,
sin∠PED=
=
=
,
解得:PE=
.
∴OC=CE=CP+PE=2+
.
∴a=2+
.
②若点P在直线y=x下方,如图2,
连接PC,过点P作PD⊥AB于D,
过点P作x轴的垂线交x轴与点M,交AB于点N,
同理可得:OM=MN,PD=1,PN=
.
∵∠PCO=∠COM=∠PMO=90°,
∴四边形PCOM是矩形.
∴OM=PC=2,OC=PM.
∴OC=PM=MN-PN=OM-PN=2-
.
∴a=2-
.
故答案为:2+
或2-
.
 设⊙P与y轴相切于点C,连接PC,则有PC⊥OC.
设⊙P与y轴相切于点C,连接PC,则有PC⊥OC.∵点P的坐标为(2,a),∴PC=2.
①若点P在直线y=x上方,如图1,
连接CP并延长交直线y=x于点E,则有CE=OC.
∵CE⊥OC,CE=OC,
∴∠COE=∠CEO=45°.
过点P作PD⊥AB于D,
由垂径定理可得:AD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△ADP中,
PD=
| PA2-AD2 |
22-(
|
在Rt△PDE中,
sin∠PED=
| PD |
| PE |
| 1 |
| PE |
| ||
| 2 |
解得:PE=
| 2 |

∴OC=CE=CP+PE=2+
| 2 |
∴a=2+
| 2 |
②若点P在直线y=x下方,如图2,
连接PC,过点P作PD⊥AB于D,
过点P作x轴的垂线交x轴与点M,交AB于点N,
同理可得:OM=MN,PD=1,PN=
| 2 |
∵∠PCO=∠COM=∠PMO=90°,
∴四边形PCOM是矩形.
∴OM=PC=2,OC=PM.
∴OC=PM=MN-PN=OM-PN=2-
| 2 |
∴a=2-
| 2 |
故答案为:2+
| 2 |
| 2 |
点评:本题考查了切线的性质、垂径定理、等腰三角形的性质、勾股定理、矩形的判定与性质等知识,还考查了分类讨论的思想,是一道易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


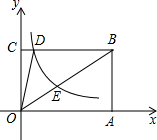 如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=
如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y= 如图,AD垂直平分BC,DE∥AB,若AB=5,则DE的长为
如图,AD垂直平分BC,DE∥AB,若AB=5,则DE的长为