题目内容
14.已知二次函数y=ax2-bx-2(a≠0)的图象的顶点在第四象限,且过点(-1,0),给出下列叙述:①式子b2>8a;
②式子a-b-2<0;
③存在实数k,满足x≤k时,函数y的值都随x的值增大而增大;
④当a-b为整数时,ab的值为1;
其中正确的是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据题意可确定a的符号,根据抛物线的对称轴的位置可确定b的符号,进而确定与x轴的交点情况即可判断①;代入(-1,0)求得a+b-2=0,进而求得a+b-2-2b=-2b>0,即可判断②;根据二次函数的性质即可判断③;根据a、b的符号,然后进一步确定a的取值范围,根据a-b为整数确定a、b的值,从而确定④.
解答 解:∵二次函数y=ax2-bx-2(a≠0)的图象的顶点在第四象限,且过点(-1,0),
∴抛物线的开口向上可得a>0,抛物线与x轴有两个交点,a+b-2=0,-$\frac{b}{2a}$>0,
∴b<0,b2-4ac>0,
∴b2-4a×(-2)>0,
∴b2>8a; 故①正确;
由a+b-2=0,b<0可知:a+b-2-2b=-2b,
即a-b-2=-2b>0,故②错误;
当x<-$\frac{b}{2a}$时,函数y的值都随x的增大而减小,
当k=-$\frac{b}{2a}$时,当x<k时,函数y的值都随x的值增大而减小;故③错误;
∵a+b-2=0,b<0,
∴b=2-a,a-b=a-(2-a)=2a-2,
于是0<a<2,
∴-2<2a-2<2,
又a-b为整数,
∴2a-2=-1,0,1,
故a=$\frac{1}{2}$,1,$\frac{3}{2}$,
b=$\frac{3}{2}$,1,$\frac{1}{2}$,
∴ab=$\frac{3}{4}$或1,故④错误.
故选B.
点评 本题主要考查了抛物线的性质(开口、对称轴等)、抛物线上点的坐标特征等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
| A. | a=$\frac{1}{3}$ | B. | a=-2 | C. | a=1 | D. | a=$\sqrt{2}$ |
9.一种细胞每过60分钟便由1个分裂成2个.经过6小时,这种细胞由1个分裂成了多少个?( )
| A. | 32 | B. | 64 | C. | 128 | D. | 16 |
6.下列各对数中,数值相等的数是( )
| A. | -|23|与|-23| | B. | -32与(-3)2 | C. | (3×2)3与3×23 | D. | -23与(-2)3 |
3.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (1,2) |
4.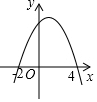 如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
 如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
如图,二次函数y=ax2+bx+c的图象与x轴交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )| A. | x<-2 | B. | x>4 | C. | -2<x<4 | D. | x>0 |
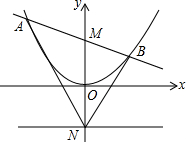 如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).
如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).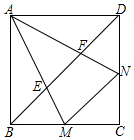 如图,在正方形ABCD中,点M,N分别在边BC,CD上,且∠MAN=45°,AM,AN分别与对角线BD交于点E,F,若EM=$\sqrt{10}$,CM=2BM,则EF的长为5$\sqrt{2}$.
如图,在正方形ABCD中,点M,N分别在边BC,CD上,且∠MAN=45°,AM,AN分别与对角线BD交于点E,F,若EM=$\sqrt{10}$,CM=2BM,则EF的长为5$\sqrt{2}$.