题目内容
4.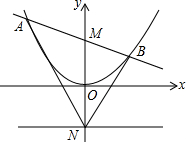 如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).
如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).(1)点P是抛物线上的一个动点,判断以点P为圆心,PM为半径的圆与直线y=-1的位置关系;
(2)若经过点M的直线与抛物线y=$\frac{1}{4}$x2的交于A、B,联结NA、NB,探索∠ANM和∠BNM之间的关系,并给出证明过程.
分析 (1)可先根据抛物线的解析式设出P点的坐标,那么可得出PM的长的表达式,P点到y=-1的长就是P点的纵坐标与-1的差的绝对值,那么可判断得出的表示PM和P到y=-1的距离的两个式子是否相等,如果相等,则y=-1是圆P的切线.
(2)可通过构建相似三角形来求解,过B,A作BR⊥直线y=-1,AH⊥直线y=-1,垂足为R,H,那么BR∥MN∥AH,根据平行线分线段成比例定理可得出BM:MA=RN:NH.(1)中已得出了AM=AH,那么同理可得出BM=BR,那么比例关系式可写成BR:AH=RN:NH,而这两组对应成比例的线段的夹角又都是直角,因此可求出∠BNR=∠ANH,根据等角的余角相等,可得出∠BNM=∠ANM.
解答 解:(1)设点P的坐标为(x0,$\frac{1}{4}$x20),则PM=$\sqrt{{{x}_{0}}^{2}+(\frac{1}{4}{{x}_{0}}^{2}-1)^{2}}$=$\frac{1}{4}$x${{\;}_{0}}^{2}$+1;
又因为点P到直线y=-1的距离为,$\frac{1}{4}$x20-(-1)=$\frac{1}{4}$x20+1
所以,以点P为圆心,PM为半径的圆与直线y=-1相切.
(2)如图,分别过点A,B作直线y=-1的垂线,垂足分别为H,R,设A(a,$\frac{1}{4}$a2),B(b,$\frac{1}{4}$b2),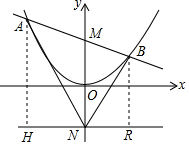 ∴AM=$\sqrt{{a}^{2}+(\frac{1}{4}{a}^{2}-1)^{2}}$=$\frac{1}{4}$a2+1,BM=$\sqrt{{b}^{2}+(\frac{1}{4}{b}^{2}-1)^{2}}$=$\frac{1}{4}$b2+1,
∴AM=$\sqrt{{a}^{2}+(\frac{1}{4}{a}^{2}-1)^{2}}$=$\frac{1}{4}$a2+1,BM=$\sqrt{{b}^{2}+(\frac{1}{4}{b}^{2}-1)^{2}}$=$\frac{1}{4}$b2+1,
∵AH=$\frac{1}{4}$a2+1,BR=$\frac{1}{4}$b2+1,
∴AM=AH,BM=BR,
∵AH,MN,BR都垂直于直线y=-1,
所以,AH∥MN∥BR,
于是$\frac{BM}{RN}=\frac{AM}{NH}$,
所以$\frac{BR}{RN}$=$\frac{AH}{HN}$,
因此,Rt△AHN∽Rt△BRN.
于是∠HNP=∠RNQ,从而∠ANM=∠BNM.
点评 本题主要考查了相似三角形的性质,平行的性质以及二次函数和一次函数的综合应用.(2)中通过构建相似三角形来求角相等是解题的关键.

| A. | 是二次三项式 | B. | 最高次项系数为3 | C. | 一次项为-x | D. | 常数项为2 |
| A. | x2+$\frac{1}{x}$ | B. | ax2+bx+c=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
| A. | 5与-(-5) | B. | 2与-$\frac{1}{2}$ | C. | -(-3)与-|-3| | D. | -$\frac{1}{4}$与-(+$\frac{1}{4}$) |
| A. | -12 | B. | 24 | C. | ±12 | D. | ±24 |
 回答下列问题:
回答下列问题: